《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

10.二次函数 $ y= ax^{2}+bx+c $ 的图象如图所示,对称轴为直线 $ x= 2 $,图象经过点(6,0),则由图象可知,当 $ y＞0 $ 时,自变量 x 的取值范围是______.

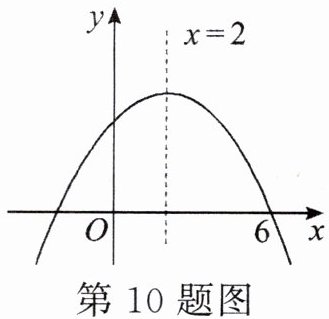
答案： -2＜x＜6

11.抛物线 $ y= ax^{2}+bx+c $ 经过点 A(-2,0),B(5,0)两点,则关于 x 的一元二次方程 $ a(x-1)^{2}+bx= b-c $ 的解是______.

答案： x₁=6,x₂=-1

12.已知抛物线 $ y= x^{2}-2(m+1)x+2(m-1) $.
(1)求证：不论 m 取何值,抛物线必与 x 轴相交于两点.
(2)若抛物线与 x 轴的一个交点为(3,0),试求 m 的值及另一个交点的坐标.
(3)若抛物线与 x 轴的两个交点分布在点(4,0)左、右两侧,求 m 的取值范围.

答案：
(1)证明:
∵Δ=4(m+1)²-8(m-1)=4m²+12＞0,
∴不论m取何值,抛物线必与x轴相交于两点.
(2)解:把(3,0)代入y=x²-2(m+1)x+2(m-1)得到m=1/4,
∴抛物线解析式为y=x²-5/2x-3/2,令y=0得到2x²-5x-3=0,
∴x=3或-1/2,
∴抛物线与x轴的另一个交点为(-1/2,0).
(3)解:由题意可得16-8(m+1)+2(m-1)＜0,
∴m＞1.

13.把一个足球垂直水平地面向上踢,时间为 t(秒)时该足球距离地面的高度 h(米)适用公式 $ h= 20t-5t^{2}(0≤t≤4) $.
(1)当 $ t= 3 $ 时,求足球距离地面的高度.
(2)当足球距离地面的高度为 10 米时,求 t.
(3)若存在实数 $ t_{1},t_{2}(t_{1}≠t_{2}) $,当 $ t= t_{1} $ 或 $ t_{2} $ 时,足球距离地面的高度都为 m(米),求 m 的取值范围.

答案：
(1)当t=3时,h=20t-5t²=20×3-5×9=15(米),
∴此时足球离地面的高度为15米.
(2)当h=10时,20t-5t²=10,即t²-4t+2=0,解得t=2+√2或t=2-√2.答:经过(2+√2)秒或(2-√2)秒时,足球距离地面的高度为10米.
(3)由题意得t₁和t₂是方程20t-5t²=m(m≥0)的两个不相等的实数根,则b²-4ac=20²-20m＞0,解得m＜20.
∴m的取值范围是0≤m＜20.

14.设二次函数 $ y= ax^{2}+bx-b-a $(a,b 是常数 $ a≠0 $).
(1)判断该二次函数图象与 x 轴的交点的个数,说明理由.
(2)若该二次函数图象的对称轴是直线 $ x= -1 $,求这个函数图象与 x 轴交点的坐标.
(3)若$ (-2,y_{1}),(-1,y_{2}) $在这个函数的图象上,且 $ y_{1}＜y_{2} $.这个二次函数图象与 x 轴的一个交点的横坐标 m($ m≠1 $),求 m 的取值范围.

答案：
(1)设y=0,
∴0=ax²+bx-b-a,
∵Δ=b²-4·a[-(a+b)]=b²+4ab+4a²=(2a+b)²≥0,
∴方程有两个不相等实数根或两个相等实根.
∴二次函数图象与x轴的交点的个数有两个或一个.
(2)
∵二次函数图象的对称轴是直线x=-1,
∴-b/(2a)=-1,
∴b=2a,
∴二次函数为y=ax²+2ax-3a,令y=0,则ax²+2ax-3a=0(a≠0),解得x₁=-3,x₂=1,
∴这个函数图象与x轴交点的坐标为(-3,0),(1,0).
(3)
∵(-2,y₁),(-1,y₂)在这个函数的图象上,且y₁＜y₂,
∴4a-2b-b-a＜a-b-b-a,即b＞3a,当x=1时,y=0,依题意,得二次函数与x轴交点为(1,0),(m,0),
∴1+m=-b/a,当a＞0时,由b＞3a,得-b/a＜-3,即1+m＜-3,即m＜-4.当a＜0时,由b＞3a,得-b/a＞-3,即1+m＞-3,即m＞-4.
∴m＜-4或m＞-4且m≠1.