第49页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
8.如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2 m,高为$2\sqrt{3}$ m,则改建后门洞的圆弧长是( )
A.$\frac{5\pi}{3}\ m$
B.$\frac{8\pi}{3}\ m$
C.$\frac{10\pi}{3}\ m$
D.$(\frac{5\pi}{3}+2)\ m$
A.$\frac{5\pi}{3}\ m$
B.$\frac{8\pi}{3}\ m$
C.$\frac{10\pi}{3}\ m$
D.$(\frac{5\pi}{3}+2)\ m$
答案:
C
9.如图,在□ABCD中,$AD= \frac{2}{3}AB$,∠BAD= 45°,以点A为圆心、AD为半径画弧交AB于点E,连接CE.若$AB= 3\sqrt{2}$,则图中阴影部分的面积是______.
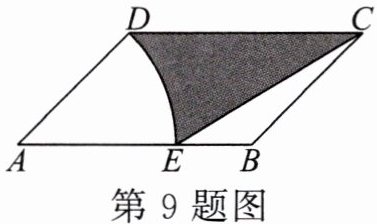

答案:
$5\sqrt{2}-\pi$
10.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC//BD,交AD于点E,连接BC.
(1)求证:AE= ED.
(2)若AB= 10,∠CBD= 36°,求$\widehat{AC}$的长.
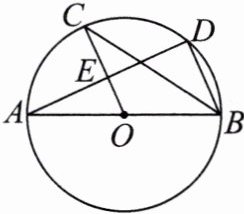
(1)求证:AE= ED.
(2)若AB= 10,∠CBD= 36°,求$\widehat{AC}$的长.

答案:
证明:
(1)
∵$AB$是$\odot O$的直径,$\therefore\angle ADB = 90^{\circ}$.$\because OC// BD$,
$\therefore\angle AEO = \angle ADB = 90^{\circ}$,即$OC⊥AD$,$\therefore AE = ED$.
(2)
∵$OC⊥AD$,$\therefore\overset{\frown}{AC}=\overset{\frown}{CD}$,$\therefore\angle ABC = \angle CBD = 36^{\circ}$,
$\therefore\angle AOC = 2\angle ABC = 2×36^{\circ}=72^{\circ}$,
$\therefore\overset{\frown}{AC}$的长$=\frac{72×\pi×5}{180}=2\pi$.
(1)
∵$AB$是$\odot O$的直径,$\therefore\angle ADB = 90^{\circ}$.$\because OC// BD$,
$\therefore\angle AEO = \angle ADB = 90^{\circ}$,即$OC⊥AD$,$\therefore AE = ED$.
(2)
∵$OC⊥AD$,$\therefore\overset{\frown}{AC}=\overset{\frown}{CD}$,$\therefore\angle ABC = \angle CBD = 36^{\circ}$,
$\therefore\angle AOC = 2\angle ABC = 2×36^{\circ}=72^{\circ}$,
$\therefore\overset{\frown}{AC}$的长$=\frac{72×\pi×5}{180}=2\pi$.
11.一个扇形的弧长为$10\pi\ cm$,面积是$120\pi\ cm^2$,求扇形的圆心角的度数.
答案:
解:设扇形的圆心角为$n^{\circ}$,半径为$R\ cm$,
则$\begin{cases}\frac{n\pi R}{180}=10\pi,\frac{n\pi R^{2}}{360}=120\pi,\end{cases}$解方程组得$\begin{cases}R = 24,\\n = 75.\end{cases}$
即扇形的圆心角为$75^{\circ}$.
则$\begin{cases}\frac{n\pi R}{180}=10\pi,\frac{n\pi R^{2}}{360}=120\pi,\end{cases}$解方程组得$\begin{cases}R = 24,\\n = 75.\end{cases}$
即扇形的圆心角为$75^{\circ}$.
12.如图,四边形ABCD中,AD//BC,∠BAD= 90°,CB= CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(1)试判断CD与⊙B的位置关系,并说明理由.
(2)若$AB= 2\sqrt{3}$,∠BCD= 60°,求图中阴影部分的面积.
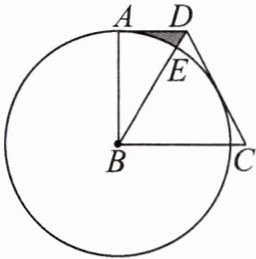
(1)试判断CD与⊙B的位置关系,并说明理由.
(2)若$AB= 2\sqrt{3}$,∠BCD= 60°,求图中阴影部分的面积.

答案:
解:
(1)过点$B$作$BF⊥CD$,垂足为$F$,
∵$AD// BC$,
∴$\angle ADB = \angle CBD$.
∵$CB = CD$,$\therefore\angle CBD = \angle CDB$,
∴$\angle ADB = \angle CDB$.在$\triangle ABD$和
$\triangle FBD$中,$\begin{cases}\angle ADB = \angle FDB,\\\angle BAD = \angle BFD,\\BD = BD,\end{cases}$
∴$\triangle ABD\cong\triangle FBD(AAS)$,$\therefore BF = BA$,则点$F$在圆$B$上,
∴$CD$与$\odot B$相切.

(2)
∵$\angle BCD = 60^{\circ}$,$CB = CD$,$\therefore\triangle BCD$是等边三角形,
$\therefore\angle CBD = 60^{\circ}$.$\because BF⊥CD$,
$\therefore\angle ABD = \angle DBF = \angle CBF = 30^{\circ}$,
$\therefore\angle ABF = 60^{\circ}$,$\because AB = BF = 2\sqrt{3}$,$\therefore AD = DF = 2$,
$\therefore$阴影部分的面积$=S_{\triangle ABD}-S_{扇形ABE}=\frac{1}{2}×2\sqrt{3}×2-\frac{30×\pi×(2\sqrt{3})^{2}}{360}=2\sqrt{3}-\pi$.
解:
(1)过点$B$作$BF⊥CD$,垂足为$F$,
∵$AD// BC$,
∴$\angle ADB = \angle CBD$.
∵$CB = CD$,$\therefore\angle CBD = \angle CDB$,
∴$\angle ADB = \angle CDB$.在$\triangle ABD$和
$\triangle FBD$中,$\begin{cases}\angle ADB = \angle FDB,\\\angle BAD = \angle BFD,\\BD = BD,\end{cases}$
∴$\triangle ABD\cong\triangle FBD(AAS)$,$\therefore BF = BA$,则点$F$在圆$B$上,
∴$CD$与$\odot B$相切.

(2)
∵$\angle BCD = 60^{\circ}$,$CB = CD$,$\therefore\triangle BCD$是等边三角形,
$\therefore\angle CBD = 60^{\circ}$.$\because BF⊥CD$,
$\therefore\angle ABD = \angle DBF = \angle CBF = 30^{\circ}$,
$\therefore\angle ABF = 60^{\circ}$,$\because AB = BF = 2\sqrt{3}$,$\therefore AD = DF = 2$,
$\therefore$阴影部分的面积$=S_{\triangle ABD}-S_{扇形ABE}=\frac{1}{2}×2\sqrt{3}×2-\frac{30×\pi×(2\sqrt{3})^{2}}{360}=2\sqrt{3}-\pi$.
查看更多完整答案,请扫码查看


