《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

1. 如图是反比例函数$ y= \frac{1}{x} $的图象,点$ A(x,y) $是反比例函数图象上任意一点,过点$ A 作 AB\perp x 轴于点 B $,连接$ OA $,则$ \triangle AOB $的面积是( )

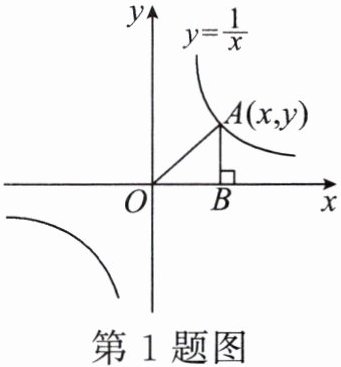
A.1
B.$ \frac{1}{2} $
C.2
D.$ \frac{3}{2} $

答案： B

2. 如图,在函数$ y= \frac{2}{x}(x＞0) 的图象上任取一点 A $,过点$ A 作 y 轴的垂线交函数 y= -\frac{8}{x}(x＜0) 的图象于点 B $,连接$ OA $,$ OB $,则$ \triangle AOB $的面积是( )

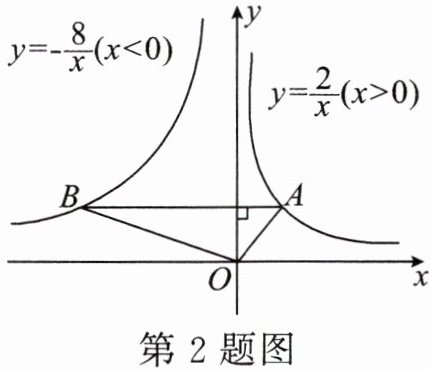
A.3
B.5
C.6
D.10

答案： B

3. 如图,在平面直角坐标系中,点$ O $为坐标原点,平行四边形$ OBAD 的顶点 B 在反比例函数 y= \frac{3}{x} $的图象上,顶点$ A 在反比例函数 y= \frac{k}{x} $的图象上,顶点$ D 在 x $轴的负半轴上.若平行四边形$ OBAD $的面积是5,则$ k $的值是( )

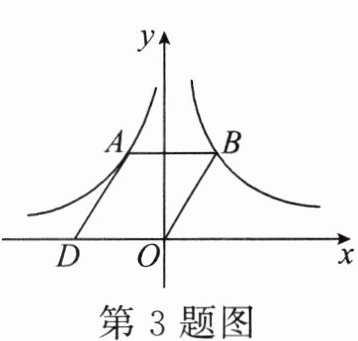
A.2
B.1
C.-1
D.-2

答案： D

4. 如图,点$ A $,$ B 是反比例函数 y= \frac{k}{x}(x＞0) $图象上的两点,过点$ A $,$ B 分别作 AC\perp x 轴于点 C $,$ BD\perp x 轴于点 D $,连接$ OA $,$ BC $.已知点$ C(2,0) $,$ BD= 2 $,$ S_{\triangle BCD}= 3 $,则$ S_{\triangle AOC}= $______.

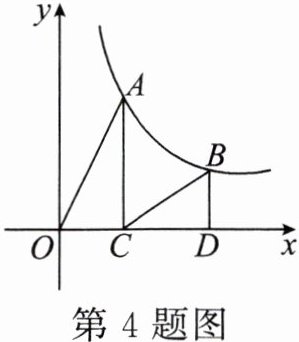
答案： 5

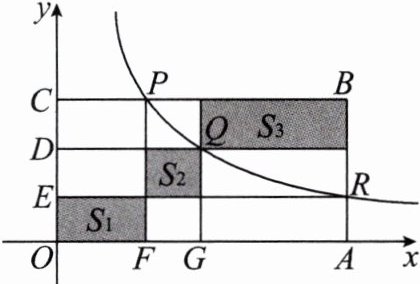
5. 点$ P $,$ Q $,$ R 在反比例函数 y= \frac{k}{x} $(常数$ k＞0 $,$ x＞0 $)图象上的位置如图所示,分别过这三个点作$ x $轴、$ y $轴的平行线.图中所构成的阴影部分面积从左到右依次为$ S_{1} $,$ S_{2} $,$ S_{3} $.若$ OE= ED= DC $,$ S_{1}+S_{3}= 27 $,则$ S_{2} $的值为______.
]

答案： $\frac{27}{5}$

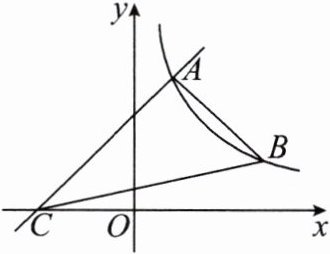
6. 如图,在平面直角坐标系中,一次函数$ y= x+2 的图象与反比例函数 y= \frac{k}{x}(x＞0) 的图象交于点 A(1,m) $,与$ x 轴交于点 C $.
(1)求点$ A $的坐标和反比例函数的解析式.
(2)点$ B $是反比例函数图象上一点且纵坐标是1,连接$ AB $,$ CB $,求$ \triangle ACB $的面积.
]

答案： 解:
(1)
∵一次函数$y=x+2$的图象过点A(1,m),
∴m=3,
∴A(1,3).
∵点A在反比例函数$y=\frac{k}{x}$(x＞0)的图象上,
∴k=1×3=3,
∴反比例函数的解析式为$y=\frac{3}{x}$.
(2)
∵点B是反比例函数图象上一点且纵坐标是1,
∴B(3,1),作BD//x轴,交直线AC于点D,则D点的纵坐标为1,代入y=x+2得,1=x+2,解得x=-1,
∴D(-1,1),
∴BD=3+1=4,
∴$S_{\triangle ABC}=\frac{1}{2}×4×3=6$.