《2025年名师面对面满分特训方案九年级数学全一册人教版台州专版》

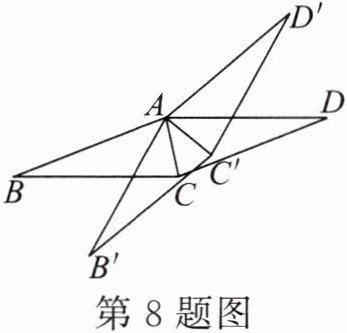
8.如图,将菱形ABCD绕点A逆时针旋转∠α得到菱形AB'C'D',∠B= ∠β.当AC平分∠B'AC'时,∠α与∠β满足的数量关系是( )

A.∠α= 2∠β
B.2∠α= 3∠β
C.4∠α+∠β= 180°
D.3∠α+2∠β= 180°

答案： C

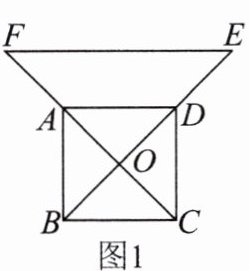
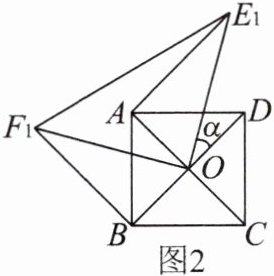
9.如图1,O为正方形ABCD的中心,分别延长OA,OD到点F,E,使OF= 2OA,OE= 2OD,连接EF.将△EOF绕点O逆时针旋转α角得到$△E_1OF_1($如图2).
(1)探究$AE_1$与$BF_1$的数量关系,并给予证明.
(2)当α= 30°时,求证$:△AOE_1$为直角三角形.

答案：
(1)解:$AE_{1}=BF_{1}$.
　证明:
∵O为正方形ABCD的中心，
∴OA=OD.
∵OF=2OA,OE=2OD,
∴OE=OF,易证△E₁AO≌△F₁BO,
∴$AE_{1}=BF_{1}$.
(2)证明:
∵取OE₁中点G,连接AG,
∵∠AOD=90°,α=30°,
∴∠E₁OA=90°-α=60°.
∵OE₁=2OA,
∴OA=OG,
∴∠E₁OA=∠AGO=∠OAG=60°,
∴AG=GE₁.
∴∠GAE₁=∠GE₁A=30°,
∴∠E₁AO=90°,
∴△AOE₁为直角三角形.

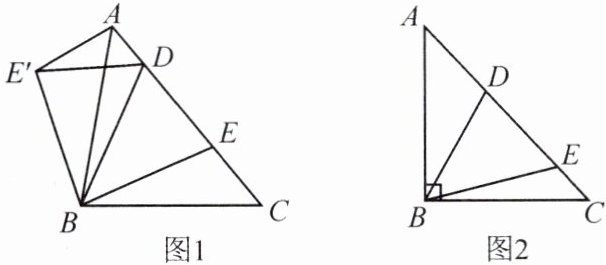
10.(1)如图1,在△ABC中,BA= BC,D,E是AC边上的两点,且满足∠DBE= $\frac{1}{2}$∠ABC(0°＜∠CBE＜$\frac{1}{2}$∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE'A(点C与点A重合,点E到点E'处),连接DE'.求证:DE'= DE.
(2)如图2,在△ABC中,BA= BC,∠ABC= 90°,D,E是AC边上的两点,且满足∠DBE= $\frac{1}{2}$∠ABC(0°＜∠CBE＜45°).求证:DE^2= AD^2+EC^2.

答案： 证明:
(1)由题意,得BE'=BE,∠E'BA=∠EBC.
∵∠DBE=$\frac{1}{2}$∠ABC,
∴∠ABD+∠EBC=$\frac{1}{2}$∠ABC.
∴∠ABD+∠E'BA=$\frac{1}{2}$∠ABC,即∠E'BD=$\frac{1}{2}$∠ABC.
∴∠E'BD=∠DBE.
∴△E'BD≌△EBD(SAS),
∴DE'=DE.
(2)由
(1)知DE'=DE.由旋转的性质知E'A=EC,∠E'AB=∠ECB.又
∵BA=BC,∠ABC=90°,
∴∠BAC=∠ACB=45°.
∴∠E'AD=∠E'AB+∠BAC=90°.
　在Rt△DE'A中,$DE'^2=AD^2+E'A^2$,
∴$DE^2=AD^2+EC^2$.