第39页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
9.⊙O 的半径为5,弦 AB//CD,AB= 6,CD= 8,则 AB 与 CD 距离为 ( )
A.7
B.8
C.7或1
D.1
A.7
B.8
C.7或1
D.1
答案:
C
10.如图所示,矩形 ABCD 与⊙O 相交于M,N,F,E,若AM= 2,DE= 1,EF= 8,则 MN 的长为 ( )
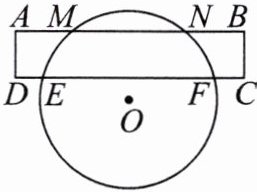
A.2
B.4
C.6
D.8

A.2
B.4
C.6
D.8
答案:
C
11.⊙O 的直径 CD= 10,AB 是⊙O 的弦,AB⊥CD,垂足为 M,OM:OC= 3:5,则 AC 的长为______.
答案:
$4\sqrt{5}$或$2\sqrt{5}$
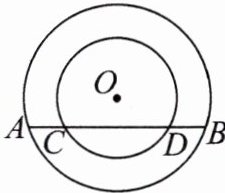
12.已知在以点 O 为圆心的两个同心圆中,大圆的弦 AB 交小圆于点 C,D(如图).
(1)求证:AC= BD.
(2)若大圆的半径 R= 10,小圆的半径 r= 8,且圆心 O 到直线 AB 的距离为 6,求 AC的长.
(1)求证:AC= BD.
(2)若大圆的半径 R= 10,小圆的半径 r= 8,且圆心 O 到直线 AB 的距离为 6,求 AC的长.

答案:
(1)证明:过点O作OE⊥AB,则AE=BE,CE=DE,
∴BE−DE=AE−CE,即AC=BD.
(2)解:由
(1)可知OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE=$\sqrt{OC^2-OE^2}=\sqrt{8^2-6^2}=2\sqrt{7}$,AE=$\sqrt{OA^2-OE^2}=\sqrt{10^2-6^2}=8$,
∴AC=AE-CE=$8-2\sqrt{7}$.
(1)证明:过点O作OE⊥AB,则AE=BE,CE=DE,
∴BE−DE=AE−CE,即AC=BD.
(2)解:由
(1)可知OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE=$\sqrt{OC^2-OE^2}=\sqrt{8^2-6^2}=2\sqrt{7}$,AE=$\sqrt{OA^2-OE^2}=\sqrt{10^2-6^2}=8$,
∴AC=AE-CE=$8-2\sqrt{7}$.
13.如图,一座圆弧形拱桥的圆心为 O,桥下水面宽度 AB 为7.2m,拱高 CD 为2.4m.
(1)求拱桥的半径.
(2)夏季雨季来临时,当水面离桥顶 C 距离为1m 时,就要禁止通行,某天暴雨后桥下水而宽度 EF 为3m,请通过计算说明是否要禁止通行.
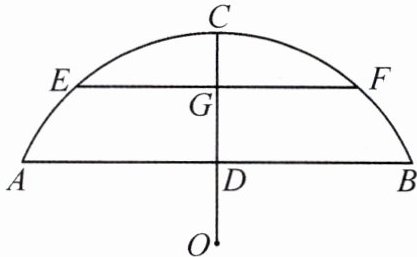
(1)求拱桥的半径.
(2)夏季雨季来临时,当水面离桥顶 C 距离为1m 时,就要禁止通行,某天暴雨后桥下水而宽度 EF 为3m,请通过计算说明是否要禁止通行.

答案:
解:
(1)如图,连接OB,
∵OC⊥AB,
∴D为AB中点.
∵AB=7.2m,
∴BD=$\frac{1}{2}$AB=3.6m.又
∵CD=2.4m,设OB=OC=rm,则OD=(r−2.4)m,在Rt△BOD中,根据勾股定理得r²=(r−2.4)²+3.6²,解得r=3.9.
答:拱桥的半径为3.9m.

(2)连接OF,
∵OC⊥EF,
∴G为EF中点,
∵EF=3m,
∴GF=$\frac{1}{2}$EF=1.5m.
∵OF=3.9m,在Rt△OFG中,OG²=OF²−GF²=3.9²−1.5²=12.96,
∴OG=$\sqrt{12.96}$=3.6m,
∴CG=OC−OG=3.9−3.6=0.3<1,
∴要禁止通行.
解:
(1)如图,连接OB,
∵OC⊥AB,
∴D为AB中点.
∵AB=7.2m,
∴BD=$\frac{1}{2}$AB=3.6m.又
∵CD=2.4m,设OB=OC=rm,则OD=(r−2.4)m,在Rt△BOD中,根据勾股定理得r²=(r−2.4)²+3.6²,解得r=3.9.
答:拱桥的半径为3.9m.

(2)连接OF,
∵OC⊥EF,
∴G为EF中点,
∵EF=3m,
∴GF=$\frac{1}{2}$EF=1.5m.
∵OF=3.9m,在Rt△OFG中,OG²=OF²−GF²=3.9²−1.5²=12.96,
∴OG=$\sqrt{12.96}$=3.6m,
∴CG=OC−OG=3.9−3.6=0.3<1,
∴要禁止通行.
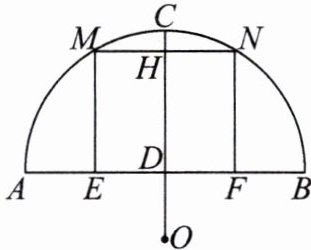
14.如图所示,某地有一座圆弧形的拱桥,桥下水面宽为7.2m,拱顶高出水面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

答案:
解:能通过.理由如下:依题意得AB=7.2,CD=2.4.连接AO,设⊙O的半径为R,在Rt△AOD中,OD=R−2.4,AD =3.6,R²=(R−2.4)²+3.6²,
∴R=3.9,OD=1.5.在Rt△OHN中,当HN=1.5时,OH=$\sqrt{ON^2-HN^2}=\sqrt{3.9^2-1.5^2}$=3.6(m),
∴HD=3.6−1.5=2.1(m).
∵2.1m>2m,
∴此货船能顺利通过.
∴R=3.9,OD=1.5.在Rt△OHN中,当HN=1.5时,OH=$\sqrt{ON^2-HN^2}=\sqrt{3.9^2-1.5^2}$=3.6(m),
∴HD=3.6−1.5=2.1(m).
∵2.1m>2m,
∴此货船能顺利通过.
查看更多完整答案,请扫码查看


