第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
6. 如图,路灯距离地面 $8$ m,身高 $1.6$ m的小明站在距离灯的底部(点 $O$)$20$ m的 $A$ 处,则小明的影子 $AM$ 长为
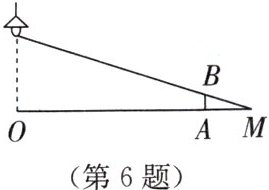
5
m.
答案:
5
7. 有三根垂直地面放置的木杆甲、乙、丙,在路灯下乙、丙的影子如图,试确定路灯灯泡的位置,再作出甲的影子.(不写作法,保留作图痕迹)
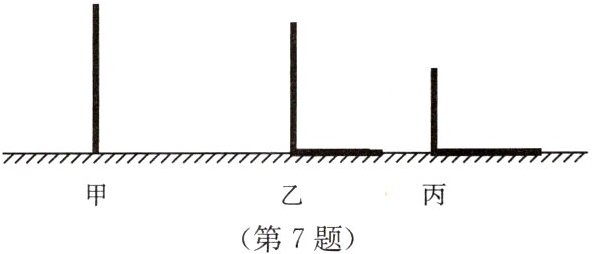

答案:
解:如图.

解:如图.

8. 如图,路灯距地面 $8$ m,身高 $1.6$ m的小明从点 $A$ 处沿 $AO$ 所在的直线行走 $14$ m到点 $B$ 时,人影(
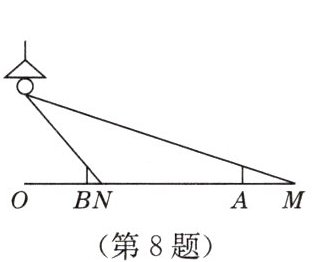
A.变长 $3.5$ m
B.变长 $2.5$ m
C.变短 $3.5$ m
D.变短 $2.5$ m
C
).
A.变长 $3.5$ m
B.变长 $2.5$ m
C.变短 $3.5$ m
D.变短 $2.5$ m
答案:
C
9. 如图,在平面直角坐标系中,点光源位于 $P(4,4)$ 处,木杆 $AB$ 两端的坐标分别为 $(0,2)$,$(6,2)$,则木杆 $AB$ 在 $x$ 轴上的影长 $CD$ 为
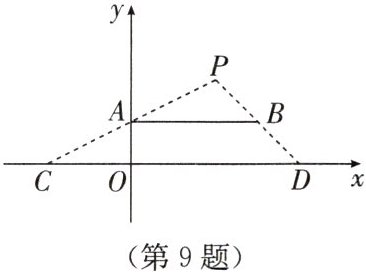
12
.
答案:
12
10. 如图,一个圆柱形无盖器皿,直径 $AD = BC = 3$,灯泡 $P$ 到 $CD$ 的距离为 $1$,点 $D$ 在灯泡 $P$ 下的投影恰好为点 $B$,点 $A$ 在灯泡 $P$ 下的投影为点 $A'$,求点 $A'$ 到 $CD$ 的距离.(注:点 $A'$,$B$,$C$ 在同一条直线上)
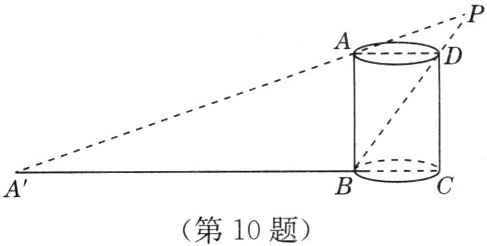

答案:
解:过点P作PP'⊥A'C交A'C的延长线于点P'.延长AD交PP'于点E(图略).
根据题意,易得△APD∽△A'PB,
△PDE∽△PBP',
∴AD/A'B = PD/PB = DE/BP'
∵DE = CP' = 1,AD = BC = 3,
∴3/A'B = 1/(3 + 1),解得A'B = 12,
∴A'C = 12 + 3 = 15.
∴点A'到CD的距离为15.
根据题意,易得△APD∽△A'PB,
△PDE∽△PBP',
∴AD/A'B = PD/PB = DE/BP'
∵DE = CP' = 1,AD = BC = 3,
∴3/A'B = 1/(3 + 1),解得A'B = 12,
∴A'C = 12 + 3 = 15.
∴点A'到CD的距离为15.
11. 如图,小欣站在路灯 $P$ 下的投影 $AB = 2.4$ m,蹲下时,其投影 $AC = 1.05$ m,小欣的身高 $AD = 1.6$ m,蹲下时的高度等于站立高度的一半,求路灯离地面的高度 $PH$.
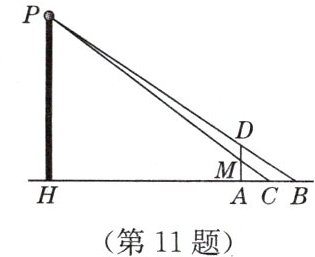

答案:
解:由题意,得AM = 1/2AD = 0.8m.
∵AD//PH,
∴∠DAC = ∠PHB.
∵∠DBA = ∠PBH,∠MCA = ∠PCH,
∴△ADB∽△HPB,△AMC∽△HPC.
∴AB∶HB = AD∶PH,AC∶AM = HC∶PH,
即2.4∶(2.4 + AH) = 1.6∶PH,
1.05∶0.8 = (1.05 + HA)∶PH.
解得PH = 7.2m.
∴路灯离地面的高度PH为7.2m.
∵AD//PH,
∴∠DAC = ∠PHB.
∵∠DBA = ∠PBH,∠MCA = ∠PCH,
∴△ADB∽△HPB,△AMC∽△HPC.
∴AB∶HB = AD∶PH,AC∶AM = HC∶PH,
即2.4∶(2.4 + AH) = 1.6∶PH,
1.05∶0.8 = (1.05 + HA)∶PH.
解得PH = 7.2m.
∴路灯离地面的高度PH为7.2m.
查看更多完整答案,请扫码查看


