《2025年新编基础训练九年级数学上册北师大版》

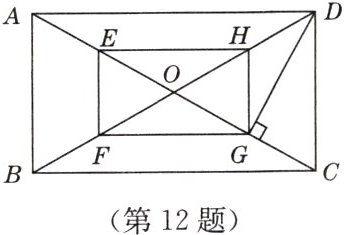
12. 如图,$O$ 是矩形 $ABCD$ 的对角线的交点,$E$,$F$,$G$,$H$ 分别是 $OA$,$OB$,$OC$,$OD$ 上的点,且 $AE = BF = CG = DH$。
(1) 求证：四边形 $EFGH$ 是矩形；
(2) 若 $E$,$F$,$G$,$H$ 分别是 $OA$,$OB$,$OC$,$OD$ 的中点,$DG \perp AC$,$OF = 2\ cm$,求矩形 $ABCD$ 的面积。

答案：
(1) 见解析；
(2) 16√3 cm²。

13. 感知 如图①,在矩形 $ABCD$ 中,点 $E$ 是边 $BC$ 的中点,将 $\triangle ABE$ 沿 $AE$ 折叠,使点 $B$ 落在矩形 $ABCD$ 内部的点 $F$ 处,延长 $AF$,交 $CD$ 于点 $G$,连接 $FC$,易证 $\angle GCF = \angle GFC$。
探究 将图①中的矩形 $ABCD$ 改为平行四边形,其他条件不变,如图②,判断 $\angle GCF = \angle GFC$ 是否仍然成立,并说明理由。
应用 如图②,若 $AB = 5$,$BC = 6$,则 $\triangle ADG$ 的周长为______。

探究
∠GCF = ∠GFC 仍然成立，理由如下：
1. 由折叠性质得：AF=AB，EF=BE，∠AFE=∠B，∠FAE=∠BAE。
2. 点E为BC中点，故BE=EC，从而EF=EC，因此∠EFC=∠ECF。
3. 四边形ABCD为平行四边形，得∠B+∠BCD=180°。
4. ∵∠AFE+∠EFG=180°且∠AFE=∠B，∴∠EFG=∠BCD。
5. ∵∠BCD=∠ECF+∠GCF，∠EFG=∠EFC+∠GFC，且∠EFC=∠ECF，
∴∠GCF=∠GFC。
应用
16

答案： 探究
∠GCF = ∠GFC 仍然成立，理由如下：
1. 由折叠性质得：AF=AB，EF=BE，∠AFE=∠B，∠FAE=∠BAE。
2. 点E为BC中点，故BE=EC，从而EF=EC，因此∠EFC=∠ECF。
3. 四边形ABCD为平行四边形，得∠B+∠BCD=180°。
4.
∵∠AFE+∠EFG=180°且∠AFE=∠B，
∴∠EFG=∠BCD。
5.
∵∠BCD=∠ECF+∠GCF，∠EFG=∠EFC+∠GFC，且∠EFC=∠ECF，

∴∠GCF=∠GFC。
应用
16
解析：
由∠GCF=∠GFC得GF=GC。设GC=x，则GF=x，DG=CD-GC=5-x，AG=AF+FG=5+x。
△ADG周长=AD+DG+AG=6+(5-x)+(5+x)=16。