《2025年新编基础训练九年级数学上册北师大版》

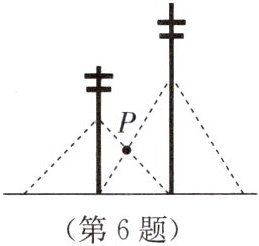
6. 相邻两根电线杆都用钢索在地面上固定,如图,一根电线杆的钢索系在离地面$4m$处,另一根电线杆的钢索系在离地面$6m$处,两根电线杆的钢索都有一根固定在另一根电线杆底部,则中间两根钢索相交点$P$离地面____2.4$m$。

答案： 2.4 解析:如图，过点P作PE⊥BC于点E.
∵CD⊥BC，AB⊥BC，
∴CD//AB.
∴△APB∽△CPD.
∴$\frac{AB}{CD}=\frac{AP}{PC}=\frac{BE}{CE}=\frac{6}{4}=\frac{3}{2}$.
∵CD//PE，
∴△BPE∽△BDC.
∴$\frac{PE}{CD}=\frac{BE}{BC}$.
∴$\frac{PE}{4}=\frac{3}{5}$.
∴PE=2.4m.
即中间两根钢索相交点P离地面2.4m.

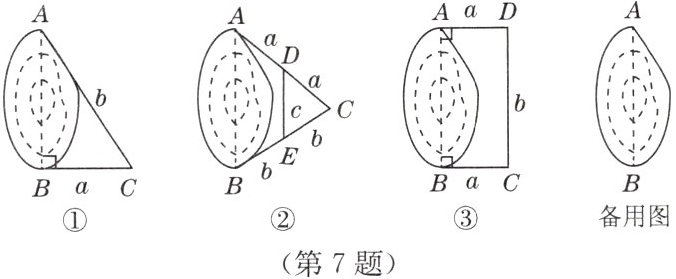
7. 如图,已知$A$,$B$两点分别位于一个池塘的两端,受条件限制无法直接测量$A$,$B$间的距离。小明利用学过的知识,设计了如下三种测量方法,如图①②③(图中$a$,$b$,$c$表示长度)。
(1)请你写出小明设计的三种测量方法中$AB$的长度：
图①中$AB = $$\sqrt{b^{2}-a^{2}}$,图②中$AB = $2c,图③中$AB = $b；
(2)请你再设计一种不同于以上三种的测量方法,画出示意图(不要求写画法),用字母标注需测量的边或角,并写出$AB$的长度。

答案：
(1)$\sqrt{b^{2}-a^{2}}$;2c;b

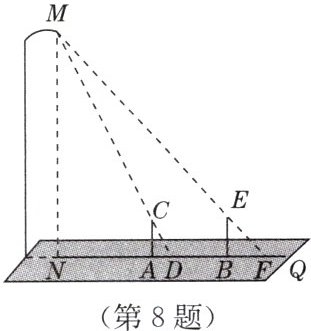
8. 晚饭后,小聪和小军在社区广场散步,小聪问小军：“你有多高？”小军一时语塞。小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高。于是,两人在灯下沿直线$NQ$移动,如图,当小聪正好站在广场的$A$点(距$N点5$块地砖长)时,其影长$AD恰好为1$块地砖长；当小军正好站在广场的$B$点(距$N点9$块地砖长)时,其影长$BF恰好为2$块地砖长。已知广场地面由边长为$0.8m$的正方形地砖铺成,小聪的身高$AC为1.6m$,$MN\perp NQ$,$AC\perp NQ$,$BE\perp NQ$。请你根据以上信息,求出小军的身高$BE$(结果精确到$0.01m$)。

答案： 解:由题意，得∠CAD=∠MND=90°，
又
∵∠CDA=∠MDN，
∴△CAD∽△MND.
∴$\frac{CA}{MN}=\frac{AD}{ND}$.
∴$\frac{1.6}{MN}=\frac{1×0.8}{(5+1)×0.8}$.
∴MN=9.6m.
经检验，MN=9.6符合题意.
∵∠EBF=∠MNF=90°，∠EFB=∠MFN，
∴△EFB∽△MFN.
∴$\frac{EB}{MN}=\frac{BF}{NF}$.
∴$\frac{EB}{9.6}=\frac{2×0.8}{(2+9)×0.8}$.
∴EB≈1.75m.
∴小军的身高BE约为1.75m.