《2025年新编基础训练九年级数学上册北师大版》

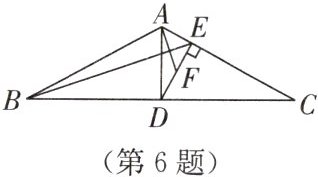
6. 如图,在△ABC中,AB= AC,D是边BC的中点,DE⊥AC,垂足为点E.
(1)求证：DE·CD= AD·CE；
(2)设F为DE的中点,连接AF,BE,求证：AF·BC= AD·BE.

答案： 证明:
(1)$\because AB=AC$,$D$是边$BC$的中点,
$\therefore AD\perp BC$,即$\angle ADC=90^{\circ}$.
$\therefore \angle ADE+\angle CDE=90^{\circ}$.
$\because DE\perp AC$,
$\therefore \angle CED=\angle AED=90^{\circ}$.
$\therefore \angle CDE+\angle DCE=90^{\circ}$.
$\therefore \angle ADE=\angle DCE$.
$\therefore \triangle AED\backsim \triangle DEC$.$\therefore \frac{DE}{CE}=\frac{AD}{CD}$.
$\therefore DE\cdot CD=AD\cdot CE$.
(2)$\because D$是边$BC$的中点,
$\therefore BD=CD=\frac{1}{2}BC$.
$\because F$为$DE$的中点,$\therefore DE=2DF$.
$\because DE\cdot CD=AD\cdot CE$,
$\therefore \frac{CE}{DF}=\frac{BC}{AD}$.
又$\because \angle BCE=\angle ADF$,
$\therefore \triangle BCE\backsim \triangle ADF$.
$\therefore \frac{BC}{AD}=\frac{BE}{AF}$.
$\therefore AF\cdot BC=AD\cdot BE$.

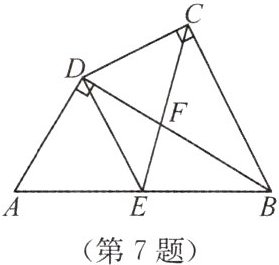
7. 如图,在四边形ABCD中,BD平分∠ABC,∠ADB= ∠DCB= 90°,E为AB的中点,CE与BD交于点F.
(1)求证：△ABD∽△DBC；
(2)求证：DE//BC；
(3)若DF：BF= 2：3,CD= 6,求DE的长.

答案：
(1)证明:$\because BD$平分$\angle ABC$,
$\therefore \angle ABD=\angle CBD$.
$\because \angle ADB=\angle DCB=90^{\circ}$,
$\therefore \triangle ABD\backsim \triangle DBC$.
(2)证明:$\because \angle ADB=90^{\circ}$,$E$为$AB$的中点,
$\therefore DE=EB=AE$.
$\therefore \angle ABD=\angle BDE$.
$\because \angle ABD=\angle CBD$,
$\therefore \angle BDE=\angle CBD$.
$\therefore DE// BC$.
(3)解:$\because DE// BC$,
$\therefore \angle DEF=\angle BCF$,$\angle EDF=\angle CBF$.
$\therefore \triangle DEF\backsim \triangle BCF$.
$\therefore \frac{DE}{BC}=\frac{DF}{BF}=\frac{2}{3}$.
设$DE=2k$,$\therefore BC=3k$.
$\because E$为$AB$的中点,$\angle ADB=90^{\circ}$,
$\therefore AB=2DE=4k$.
$\because \triangle ABD\backsim \triangle DBC$,$\therefore \frac{AB}{DB}=\frac{DB}{BC}$.
$\therefore DB^{2}=AB\cdot BC=4k× 3k=12k^{2}$.
$\because \angle BCD=90^{\circ}$,$CD=6$,
$\therefore BC^{2}+CD^{2}=BD^{2}$.
$\therefore (3k)^{2}+6^{2}=12k^{2}$,
解得$k=2\sqrt{3}$(负值舍去).
$\therefore DE=4\sqrt{3}$.

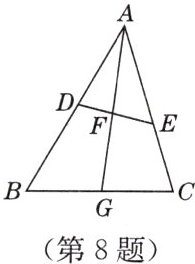
8. 如图,在△ABC中,点D,E分别在边AB,AC上,∠AED= ∠B,AG分别交线段DE,BC于点F,G,且AD：AC= DF：CG.求证：
(1)AG平分∠BAC；
(2)EF·CG= DF·BG.

答案： 证明:
(1)$\because \angle DAE+\angle AED+\angle ADE=180^{\circ}$,
$\angle BAC+\angle B+\angle C=180^{\circ}$,$\angle AED=\angle B$,
$\therefore \angle ADE=\angle C$.
又$\because AD:AC=DF:CG$,$\therefore \triangle ADF\backsim \triangle ACG$.
$\therefore \angle DAF=\angle CAG$.$\therefore AG$平分$\angle BAC$.
(2)$\because \angle AEF=\angle B$,
$\angle EAF=\angle BAG$,
$\therefore \triangle AEF\backsim \triangle ABG$.$\therefore \frac{EF}{BG}=\frac{AF}{AG}$.
$\because \triangle ADF\backsim \triangle ACG$,$\therefore \frac{DF}{CG}=\frac{AF}{AG}$.
$\therefore \frac{EF}{BG}=\frac{DF}{CG}$.$\therefore EF\cdot CG=DF\cdot BG$.

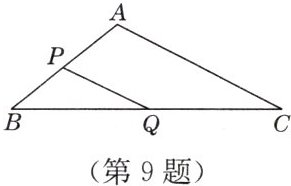
9. 如图,在△ABC中,AB= 8 cm,BC= 16 cm,点P从点A开始沿边AB向点B以2 cm/s的速度移动,点Q从点B开始沿边BC向点C以4 cm/s的速度移动.如果点P,Q分别从点A,B同时出发,几秒后,△PBQ与△ABC相似？

答案： 解:设$x\ s$后,$\triangle PBQ$与$\triangle ABC$相似,
则$AP=2x\ cm$,$BQ=4x\ cm$.
$\because AB=8\ cm$,
$\therefore BP=AB-AP=(8-2x)\ cm$.
$\because \angle B$是公共角,
$\therefore$分$\triangle PBQ\backsim \triangle ABC$和$\triangle PBQ\backsim \triangle CBA$两种情况.
①当$\triangle PBQ\backsim \triangle ABC$时,
$\frac{BP}{BA}=\frac{BQ}{BC}$,即$\frac{8-2x}{8}=\frac{4x}{16}$,解得$x=2$;
②当$\triangle PBQ\backsim \triangle CBA$时,$\frac{BP}{BC}=\frac{BQ}{BA}$,即$\frac{8-2x}{16}=\frac{4x}{8}$,
解得$x=0.8$.
$\therefore 2\ s$或$0.8\ s$后,$\triangle PBQ$与$\triangle ABC$相似.