第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
5. 如图所示,地面上有一个不规则的封闭图形,为求得它的面积,小明设计了如下的一个方案:
①在此封闭图形内画出一个半径为 1 m 的圆.
②在此封闭图形外闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
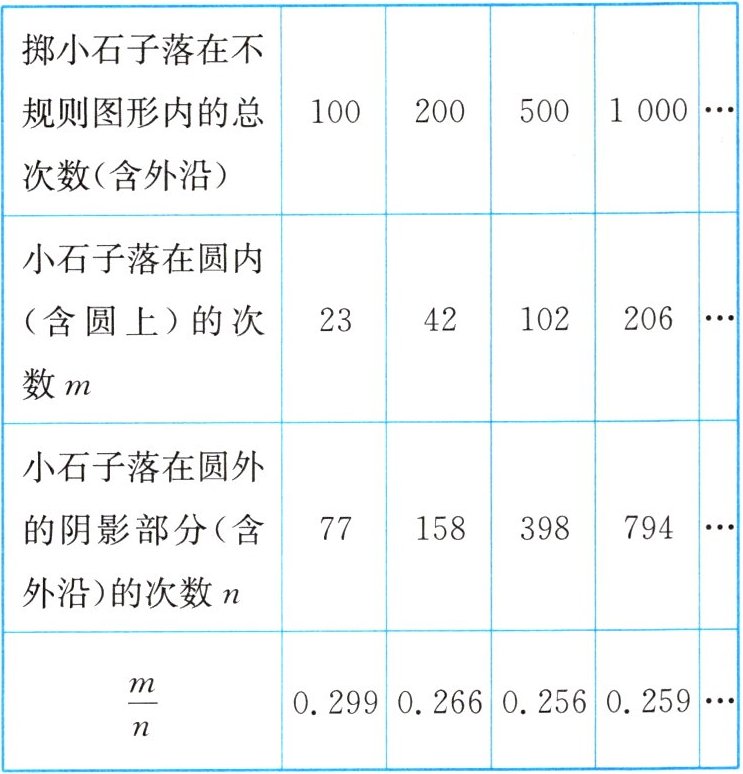
(1)通过以上信息,可以发现当投掷的次数很多时,$\frac{m}{n}$ 的值越来越接近
(2)若以小石子所落的有效区域为总数(即 $ m + n $),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在
(3)请你利用(2)中所得的频率,估计整个封闭图形的面积是多少平方米?(结果保留 $ \pi $)
①在此封闭图形内画出一个半径为 1 m 的圆.
②在此封闭图形外闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:

(1)通过以上信息,可以发现当投掷的次数很多时,$\frac{m}{n}$ 的值越来越接近
0.26
;(结果精确到 0.01)(2)若以小石子所落的有效区域为总数(即 $ m + n $),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在
0.2
附近;(结果精确到 0.1)(3)请你利用(2)中所得的频率,估计整个封闭图形的面积是多少平方米?(结果保留 $ \pi $)

解:设封闭图形的面积为a,根据题意得$\frac{π}{a}=0.2$,$\therefore a=5π$.答:估计整个封闭图形的面积是$5π\ m^2$.
答案:
(1)0.26
(2)0.2 解析:206÷1000≈0.2,
∴随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在0.2附近.故答案为0.2.
(3)解:设封闭图形的面积为a,根据题意得$\frac{π}{a}=0.2$,$\therefore a=5π$.答:估计整个封闭图形的面积是$5π\ m^2$.
(1)0.26
(2)0.2 解析:206÷1000≈0.2,
∴随着投掷次数的增大,小石子落在圆内(含圆上)的频率稳定在0.2附近.故答案为0.2.
(3)解:设封闭图形的面积为a,根据题意得$\frac{π}{a}=0.2$,$\therefore a=5π$.答:估计整个封闭图形的面积是$5π\ m^2$.
6. (1)一个不透明的口袋中装有若干个除颜色外其他都相同的红球与黄球. 在这个口袋中先放入 2 个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回口袋中,再继续摸球,全班一共进行了 400 次这样的摸球试验. 如果知道摸出白球 40 次,你能估计在未放入白球前,口袋中原来共有多少个球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出 8 个球,画上记号放回盒中,再进行摸球试验. 摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,然后放回盒中搅匀,再继续摸球、记录、放回盒中.
统计结果:摸球试验一共进行了 50 次,统计结果如下表:

由上述摸球试验推算:
①盒中红球、黄球各占球的总个数的百分比;
②盒中有多少个红球?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出 8 个球,画上记号放回盒中,再进行摸球试验. 摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,然后放回盒中搅匀,再继续摸球、记录、放回盒中.
统计结果:摸球试验一共进行了 50 次,统计结果如下表:

由上述摸球试验推算:
①盒中红球、黄球各占球的总个数的百分比;
②盒中有多少个红球?
答案:
(1)能.设口袋中原来共有x个球,$\frac{40}{400}=\frac{2}{2+x}$,解得$x=18$.经检验,$x=18$是所列方程的解,且符合题意.因此,估计在未放入白球前,口袋中原来共有18个球.
(2)①盒中红球占总球数的百分比是$\frac{18+2}{50}=\frac{20}{50}=40\%$,盒中黄球占总球数的百分比是$\frac{28+2}{50}=\frac{30}{50}=60\%$.
②设盒中有y个球,由题意得$\frac{2+2}{50}=\frac{8}{y}$,解得$y=100$.经检验,$y=100$是所列方程的解,且符合题意.$100×40\%=40$(个),即盒中有40个红球.
(1)能.设口袋中原来共有x个球,$\frac{40}{400}=\frac{2}{2+x}$,解得$x=18$.经检验,$x=18$是所列方程的解,且符合题意.因此,估计在未放入白球前,口袋中原来共有18个球.
(2)①盒中红球占总球数的百分比是$\frac{18+2}{50}=\frac{20}{50}=40\%$,盒中黄球占总球数的百分比是$\frac{28+2}{50}=\frac{30}{50}=60\%$.
②设盒中有y个球,由题意得$\frac{2+2}{50}=\frac{8}{y}$,解得$y=100$.经检验,$y=100$是所列方程的解,且符合题意.$100×40\%=40$(个),即盒中有40个红球.
查看更多完整答案,请扫码查看


