《2025年通城学典课时作业本七年级数学上册人教版》

9. 有下列算式：① $-(-2)^4= 16$；② $-5÷\frac{1}{5}= -5$；③ $\frac{2^3}{3}= \frac{8}{27}$；④ $(-3)^2×(-\frac{1}{3})= -3$；⑤ $-6^3= -18$.其中,错误的个数为( )

A.2
B.3
C.4
D.5

答案： C

10. 如果$|a|= 4$,$|b|= 3$,且$a＜0＜b$,那么$(a+b)^3= $______.

答案： -1

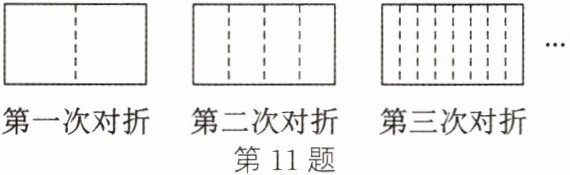
11. 将一张长方形纸片按如图所示的方式对折,第一次对折后可得到1条折痕(图中虚线),第二次对折后可得到3条折痕,第三次对折后可得到7条折痕,那么第七次对折后可得到______条折痕.
]

答案： 127

12. 观察下列等式：$3^1= 3$,$3^2= 9$,$3^3= 27$,$3^4= 81$,$3^5= 243$,$3^6= 729$,…,则$3^{2025}$的个位数字是______.

答案： 3 解析:因为$3^1=3$,$3^2=9$,$3^3=27$,$3^4=81$,$3^5=243$,$3^6=729$,$\cdots$,所以3的正整数次方的个位数字按3,9,7,1的顺序进行循环.因为$2025÷4=506\cdots\cdots1$,所以$3^{2025}$的个位数字是3.

13. 计算：
(1)$-(-3)^4÷(-27)$；
(2)$0.125^3×8^3$；
(3)$-2^{2025}+(-2)^{2025}$；
(4)$(-2)^2 - 2^2 + (-\frac{2}{3})^2 - \frac{2}{3^2}$.

答案： （1）3 （2）1 （3）$-2^{2026}$ （4）$\frac{2}{9}$

14. 已知$a$,$b$为有理数,且$|a+4|+(b-3)^2= 0$,求$(a+b)^{2025}$的值.

答案： 由题意,得$a+4=0$,$b-3=0$,解得$a=-4$,$b=3$.所以$(a+b)^{2025}=(-4+3)^{2025}=-1$

15. (教材P53例4变式)观察下列各组数：
① $-1,2,-4,8,-16,32,…$；
② $0,3,-3,9,-15,33,…$；
③ $-2,4,-8,16,-32,64,…$.
(1)第①组数是按什么规律排列的？
(2)第②③组数分别与第①组数有什么数量关系？
(3)取每组数的第8个数,计算这三个数的和.

答案： （1）相邻的两个数中,后面一个数与前面一个数相除的商是-2 （2）对比①②③三组中对应位置的数,第②组数比第①组对应位置的数大1,第③组数是第①组对应位置的数的2倍 （3）由（2）,得这三个数的和为$2^7+(2^7+1)+(2^7×2)=513$