《2025年通城学典课时作业本七年级数学上册人教版》

1. 有一列数$a_1,a_2,a_3,…,a_n$,其中$a_1= -1$,$a_2= \frac{1}{1-a_1}$,$a_3= \frac{1}{1-a_2}$,…$$,$a_n= \frac{1}{1-a_{n-1}}$,则$a_1× a_2× a_3×…× a_{2024}× a_{2025}$的结果为 ( )

A.$-1$
B.$\frac{1}{2}$
C.$2022$
D.$-2022$

答案： A 解析:因为$a_{1}=-1$,所以$a_{2}=\frac{1}{1-a_{1}}=\frac{1}{2}$,$a_{3}=\frac{1}{1-a_{2}}=2$,$a_{4}=\frac{1}{1-a_{3}}=-1$,…所以每三个数为一组循环.因为易得$a_{1}a_{2}a_{3}=-1$,所以$a_{1}× a_{2}× a_{3}×\cdots× a_{2024}× a_{2025}=(a_{1}a_{2}a_{3})^{675}=(-1)^{675}=-1$.

2. 观察下面的变化规律：$\frac{2}{1×3}= 1-\frac{1}{3}$,$\frac{2}{3×5}= \frac{1}{3}-\frac{1}{5}$,$\frac{2}{5×7}= \frac{1}{5}-\frac{1}{7}$,$\frac{2}{7×9}= \frac{1}{7}-\frac{1}{9}$,…$$。根据上面的规律计算：$\frac{2}{1×3}+\frac{2}{3×5}+\frac{2}{5×7}+…+\frac{2}{2023×2025}= $______。

答案： $\frac{2024}{2025}$

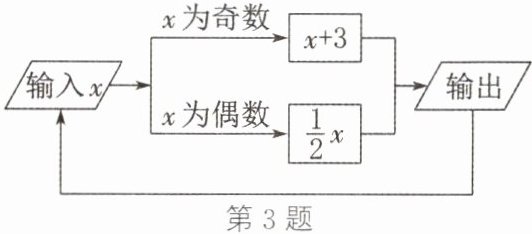
3. 有一数值转换器,原理如图所示。若开始输入$x$的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…$$,则第2026次输出的结果是 ( )


A.$8$
B.$4$
C.$2$
D.$1$

答案： D 解析:若开始输入$x$的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,第三次输出的结果是2,第四次输出的结果是1,第五次输出的结果是4,第六次输出的结果是2,第七次输出的结果是1,第八次输出的结果是4,第九次输出的结果是2,第十次输出的结果是1……故从第二次开始,每3次一循环.因为$(2026-1)÷3=675$,所以第2026次输出的结果是1.

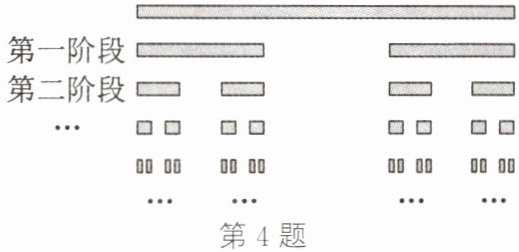
4. 如图,取一条长度为1的线段,将它三等分,去掉中间一段,剩下两段,这称为第一阶段；然后将剩下的两段再三等分,各去掉中间一段,剩下更短的四段,这称为第二阶段……$$将这样的操作重复下去,那么经过第十阶段后,剩下线段的长度之和为 ( )


A.$1-\frac{1}{3^{11}}$
B.$\frac{2^{11}}{3^{11}}$
C.$1-\frac{1}{3^{10}}$
D.$\frac{2^{10}}{3^{10}}$

答案： D 解析:由题图可知,第一阶段时,剩下线段的长度之和为$\frac{2}{3}$;第二阶段时,剩下线段的长度之和为$\frac{2}{3}×\frac{2}{3}=(\frac{2}{3})^{2}$;第三阶段时,剩下线段的长度之和为$\frac{2}{3}×\frac{2}{3}×\frac{2}{3}=(\frac{2}{3})^{3}$……以此类推,当到达第$n$($n$为正整数)阶段时,剩下线段的长度之和为$(\frac{2}{3})^{n}$.所以经过第十阶段后,剩下线段的长度之和为$(\frac{2}{3})^{10}=\frac{2^{10}}{3^{10}}$.

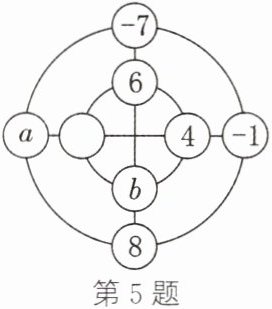
5. 小刚同学设计了一种“幻圈”游戏,将$-1$,$2$,$-3$,$4$,$-5$,$6$,$-7$,$8$分别填入如图所示的圆圈内,使横、竖以及内外两圈上的4个数之和都相等。他已经将$-1$,$4$,$6$,$-7$,$8$这五个数填入了圆圈内,则图中$a+b$的值为 ( )


A.$-6$
B.$-3$
C.$-4$
D.$-1$

答案： B

6. 如图,下列图形中的三个数之间均有相同的规律。根据此规律可知,图形中$n$的值是______。

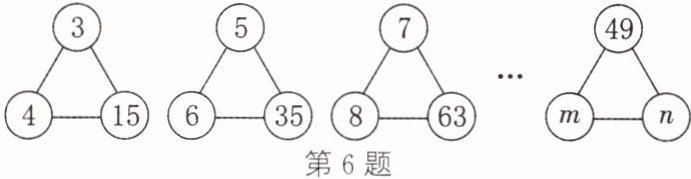
答案： 2499

7. 我国南宋数学家杨辉用如图所示的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”。请观察图中数的排列规律,则$a+b+c$的值为______。

答案： 41