《2025年通城学典课时作业本七年级数学上册人教版》

13. 先找规律,再填数：$\frac{1}{1}+\frac{1}{2}-1= \frac{1}{2}$,$\frac{1}{3}+\frac{1}{4}-\frac{1}{2}= \frac{1}{12}$,$\frac{1}{5}+\frac{1}{6}-\frac{1}{3}= \frac{1}{30}$,$\frac{1}{7}+\frac{1}{8}-\frac{1}{4}= \frac{1}{56}$,…,则$\frac{1}{2025}+\frac{1}{2026}-$______$=\frac{1}{2025×2026}$.

答案： $\frac{1}{1013}$ 解析：通过观察可知，每个等式左边前面的两个分数的分母为两个连续的正整数，第三个分数为第二个分数的2倍，等式右边为等式左边前面两个分数的乘积. 由此可知，$\frac{1}{2025}+\frac{1}{2026}-\frac{1}{1013}=\frac{1}{2025×2026}$.

14. 在某班举行的“数学晚会”上,A,B,C,D,E五名同学的手上各拿着一张卡片,卡片上分别写着2,$-\frac{1}{2}$,0,-3,$\frac{1}{6}$. 主持人按照卡片上的这些数的特征,将这五名同学分成两组或者三组来表演节目(每组人数不限). 如果让你来分,那么你会如何分组呢？

答案： 答案不唯一，如按正数、非正数分成两组，分别是$2,\frac{1}{6}$和$-\frac{1}{2},0,-3$

15. 观察下列各数：$\frac{1}{2},-\frac{2}{3},\frac{1}{4},-\frac{4}{5},\frac{1}{6},-\frac{6}{7},…$. 请你找出其中的规律,并解答问题：
(1)第9个数是______,第14个数是______；
(2)第2025个数是多少？

答案： （1）$\frac{1}{10}$ $-\frac{14}{15}$ （2）$\frac{1}{2026}$

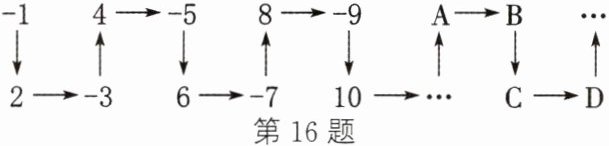
16. 将一串有理数按如图所示的规律排列,解答下列问题：
(1)在A位置上的数是正数还是负数？
(2)A,B,C,D中哪些位置上的数是负数？
(3)第2025个数是正数还是负数？对应A,B,C,D中的哪个位置？

答案： （1）在A位置上的数是正数 （2）在B和D位置上的数是负数 （3）第2025个数是负数 对应B位置