《2025年玩转全课程八年级数学全一册浙教版》

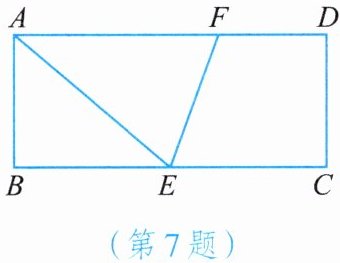
7. 如图,在矩形ABCD中,E为BC边的中点,$∠AEC$的平分线交AD边于点F,若$AB= 3,AD= 8$,则FD的长为(C)

A.1
B.2
C.3
D.4

答案： 解：
∵四边形ABCD是矩形，
∴AD=BC=8，AB=CD=3，AD//BC，∠B=90°。
∵E为BC中点，
∴BE=EC=4。
在Rt△ABE中，AE=√(AB²+BE²)=√(3²+4²)=5。
∵AD//BC，
∴∠AFE=∠FEC。
∵EF平分∠AEC，
∴∠AEF=∠FEC。
∴∠AFE=∠AEF，
∴AF=AE=5。
∵AD=8，
∴FD=AD-AF=8-5=3。
答案：C

8. 如图,在平面直角坐标系中,O为坐标原点,四边形ABCD是矩形,顶点A,B,C,D的坐标分别为$(-1,0),(5,0),(5,2),(-1,2)$,点$E(3,0)$在x轴上,点P在CD边上运动,使$△OPE$为等腰三角形,则满足条件的P点有____3个.

答案： 解：设点P坐标为$(x,2)$，其中$-1 \leq x \leq 5$。
情况1：OP=OE
$OE=3$，$OP=\sqrt{x^2+2^2}=3$
$x^2+4=9$，$x^2=5$，$x=\pm\sqrt{5}$
$x=\sqrt{5}\approx2.236$（在范围内），$x=-\sqrt{5}\approx-2.236$（舍去），得$P(\sqrt{5},2)$。
情况2：PE=OE
$PE=\sqrt{(x-3)^2+2^2}=3$
$(x-3)^2+4=9$，$(x-3)^2=5$，$x=3\pm\sqrt{5}$
$x=3+\sqrt{5}\approx5.236$（舍去），$x=3-\sqrt{5}\approx0.764$（在范围内），得$P(3-\sqrt{5},2)$。
情况3：OP=PE
$\sqrt{x^2+4}=\sqrt{(x-3)^2+4}$
$x^2=(x-3)^2$，$x^2=x^2-6x+9$，$6x=9$，$x=1.5$（在范围内），得$P(1.5,2)$。
综上，满足条件的P点有3个。
3

9. 如图,已知$MN// PQ$,EF与MN,PQ分别交于A,C两点,过A,C两点作两组内错角的平分线,分别交于点B,D,则四边形ABCD是矩形.

答案： 解：
∵MN//PQ，
∴∠MAC=∠ACQ，∠ACP=∠NAC。
∵AB平分∠MAC，CD平分∠ACQ，
∴∠BAC=∠MAC/2，∠DCA=∠ACQ/2，
∴∠BAC=∠DCA，
∴AB//CD。
∵AD平分∠NAC，BC平分∠ACP，
∴∠CAD=∠NAC/2，∠BCA=∠ACP/2，
∴∠CAD=∠BCA，
∴AD//BC，
∴四边形ABCD是平行四边形。
∵∠MAC+∠NAC=180°，
∴∠BAC+∠CAD=（∠MAC+∠NAC）/2=90°，
即∠BAD=90°，
∴四边形ABCD是矩形。
答案：矩形

已知:如图1,在平行四边形ABCD中,AC=BD,求证:平行四边形ABCD是矩形.
(1)在横线上填空,补全已知和求证.
(2)按王晓的想法写出证明过程.
证明: ∵四边形ABCD是平行四边形, ∴AD//CB, AD=BC. 在△ADC和△BCD中, ∵AC=BD, AD=BC, CD=DC, ∴△ADC≌△BCD(SSS), ∴∠ADC=∠BCD. 又∵AD//CB, ∴∠ADC+∠BCD=180°, ∴∠ADC=∠BCD=90°, ∴平行四边形ABCD是矩形.

答案：
(1) AC=BD 矩形
(2) 证明:
∵四边形ABCD是平行四边形,
∴AD//CB, AD=BC. 在△ADC和△BCD中,
∵AC=BD, AD=BC, CD=DC,
∴△ADC≌△BCD(SSS),
∴∠ADC=∠BCD. 又
∵AD//CB,
∴∠ADC+∠BCD=180°,
∴∠ADC=∠BCD=90°,
∴平行四边形ABCD是矩形.