2025年玩转全课程八年级数学全一册浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年玩转全课程八年级数学全一册浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表所示:
|班级|参加人数|中位数|方差|平均数|
|甲|55|149|1.91|135|
|乙|55|151|1.10|135|
根据上表得出以下结论:①甲、乙两班学生的平均成绩相同;②乙班优秀的人数比甲班多(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.其中正确的是(
A.①②③
B.①②
C.①③
D.②③
|班级|参加人数|中位数|方差|平均数|
|甲|55|149|1.91|135|
|乙|55|151|1.10|135|
根据上表得出以下结论:①甲、乙两班学生的平均成绩相同;②乙班优秀的人数比甲班多(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.其中正确的是(
A
)A.①②③
B.①②
C.①③
D.②③
答案:
解:①甲、乙两班的平均数均为135,故平均成绩相同,正确;
②甲班中位数为149,说明至少有28人输入汉字个数≤149,优秀人数≤55-28=27人;乙班中位数为151,说明至少有28人输入汉字个数≥151,优秀人数≥28人,故乙班优秀人数比甲班多,正确;
③甲班方差1.91>乙班方差1.10,所以甲班成绩波动比乙班大,正确。
结论:①②③均正确。
答案:A
②甲班中位数为149,说明至少有28人输入汉字个数≤149,优秀人数≤55-28=27人;乙班中位数为151,说明至少有28人输入汉字个数≥151,优秀人数≥28人,故乙班优秀人数比甲班多,正确;
③甲班方差1.91>乙班方差1.10,所以甲班成绩波动比乙班大,正确。
结论:①②③均正确。
答案:A
8. 样本数据10,10,x,8的众数和平均数相同,则12,12,x+2,10这组数据的标准差是
$\sqrt{2}$
.
答案:
解:
情况1:众数为10时,
平均数为$\frac{10+10+x+8}{4}=10$,
解得$x=12$。
情况2:众数为8时,
$x=8$,平均数为$\frac{10+10+8+8}{4}=9$,
众数≠平均数,舍去。
计算新数据的标准差:
$x=12$,新数据为12,12,14,10。
平均数$\overline{x}=\frac{12+12+14+10}{4}=12$。
方差$s^2=\frac{(12-12)^2+(12-12)^2+(14-12)^2+(10-12)^2}{4}=2$。
标准差$s=\sqrt{2}$。
$\sqrt{2}$
情况1:众数为10时,
平均数为$\frac{10+10+x+8}{4}=10$,
解得$x=12$。
情况2:众数为8时,
$x=8$,平均数为$\frac{10+10+8+8}{4}=9$,
众数≠平均数,舍去。
计算新数据的标准差:
$x=12$,新数据为12,12,14,10。
平均数$\overline{x}=\frac{12+12+14+10}{4}=12$。
方差$s^2=\frac{(12-12)^2+(12-12)^2+(14-12)^2+(10-12)^2}{4}=2$。
标准差$s=\sqrt{2}$。
$\sqrt{2}$
9. 一运动员进行了6次跳远测试,其成绩的平均数为7.8m,方差为$\frac{1}{60}m^{2}$.如果他再跳两次,成绩分别为7.6m,8.0m,那么这组跳远成绩的方差会
变大
.(填“变大”“不变”或“变小”)
答案:
解:已知6次跳远成绩的平均数为7.8m,方差为$\frac{1}{60}m^{2}$。
加入两次成绩7.6m、8.0m后,总次数为8次。
新平均数$\bar{x}=\frac{6×7.8 + 7.6 + 8.0}{8}=\frac{46.8 + 15.6}{8}=\frac{62.4}{8}=7.8m$。
原方差$s^{2}_{1}=\frac{1}{6}\sum_{i=1}^{6}(x_{i}-7.8)^{2}=\frac{1}{60}$,则$\sum_{i=1}^{6}(x_{i}-7.8)^{2}=6×\frac{1}{60}=\frac{1}{10}$。
新方差$s^{2}_{2}=\frac{1}{8}[\sum_{i=1}^{6}(x_{i}-7.8)^{2}+(7.6 - 7.8)^{2}+(8.0 - 7.8)^{2}]$
$=\frac{1}{8}[\frac{1}{10}+(-0.2)^{2}+(0.2)^{2}]$
$=\frac{1}{8}[\frac{1}{10}+0.04 + 0.04]$
$=\frac{1}{8}[\frac{1}{10}+0.08]=\frac{1}{8}×0.18=\frac{9}{400}=0.0225$。
原方差$\frac{1}{60}\approx0.0167$,因为$0.0225>0.0167$,所以方差变大。
变大
加入两次成绩7.6m、8.0m后,总次数为8次。
新平均数$\bar{x}=\frac{6×7.8 + 7.6 + 8.0}{8}=\frac{46.8 + 15.6}{8}=\frac{62.4}{8}=7.8m$。
原方差$s^{2}_{1}=\frac{1}{6}\sum_{i=1}^{6}(x_{i}-7.8)^{2}=\frac{1}{60}$,则$\sum_{i=1}^{6}(x_{i}-7.8)^{2}=6×\frac{1}{60}=\frac{1}{10}$。
新方差$s^{2}_{2}=\frac{1}{8}[\sum_{i=1}^{6}(x_{i}-7.8)^{2}+(7.6 - 7.8)^{2}+(8.0 - 7.8)^{2}]$
$=\frac{1}{8}[\frac{1}{10}+(-0.2)^{2}+(0.2)^{2}]$
$=\frac{1}{8}[\frac{1}{10}+0.04 + 0.04]$
$=\frac{1}{8}[\frac{1}{10}+0.08]=\frac{1}{8}×0.18=\frac{9}{400}=0.0225$。
原方差$\frac{1}{60}\approx0.0167$,因为$0.0225>0.0167$,所以方差变大。
变大
10. 甲、乙两名运动员的射击成绩(靶心为10环)如下表所示(不完全):
|次序|1|2|3|4|5|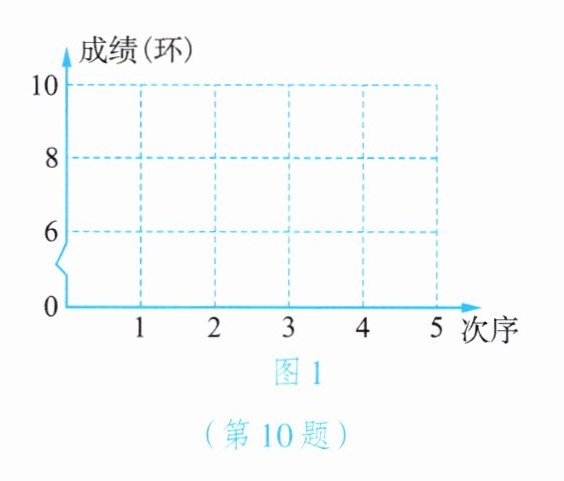
|甲|10|8|9|10|8|
|乙|10|9|9|a|b|
(1) 请在图1中用折线统计图把甲的成绩表示出来.
(2) 若甲、乙两名运动员射击成绩的平均值相等,则a + b的值是
(3) 在(2)的条件下,当乙的成绩比甲稳定时,请列出a,b所有可能的值.
|次序|1|2|3|4|5|

|甲|10|8|9|10|8|
|乙|10|9|9|a|b|
(1) 请在图1中用折线统计图把甲的成绩表示出来.
(图略,在图1中依次描出(1,10)、(2,8)、(3,9)、(4,10)、(5,8)并连接成折线)
(2) 若甲、乙两名运动员射击成绩的平均值相等,则a + b的值是
17
.(3) 在(2)的条件下,当乙的成绩比甲稳定时,请列出a,b所有可能的值.
$a=8$,$b=9$;$a=9$,$b=8$
答案:
(1)(图略,在图1中依次描出(1,10)、(2,8)、(3,9)、(4,10)、(5,8)并连接成折线)
(2)解:甲的平均成绩为$\frac{10 + 8 + 9 + 10 + 8}{5} = \frac{45}{5} = 9$(环)
因为甲、乙平均值相等,所以乙的平均成绩也为9环,即$\frac{10 + 9 + 9 + a + b}{5} = 9$
解得$10 + 9 + 9 + a + b = 45$,$a + b = 17$
(3)解:甲成绩的方差$s^{2}_{甲}=\frac{1}{5}[(10 - 9)^{2}+(8 - 9)^{2}+(9 - 9)^{2}+(10 - 9)^{2}+(8 - 9)^{2}]=\frac{1}{5}(1 + 1 + 0 + 1 + 1)=\frac{4}{5}=0.8$
乙成绩的方差$s^{2}_{乙}=\frac{1}{5}[(10 - 9)^{2}+(9 - 9)^{2}+(9 - 9)^{2}+(a - 9)^{2}+(b - 9)^{2}]=\frac{1}{5}[1 + 0 + 0 + (a - 9)^{2}+(b - 9)^{2}]$
因为$a + b = 17$,所以$b = 17 - a$,代入得$s^{2}_{乙}=\frac{1}{5}[1 + (a - 9)^{2}+(8 - a)^{2}]$
要使乙比甲稳定,则$s^{2}_{乙}<0.8$,即$(a - 9)^{2}+(8 - a)^{2}<3$
整数解为$a = 8$,$b = 9$或$a = 9$,$b = 8$
答案:(2)17;(3)$a=8$,$b=9$;$a=9$,$b=8$
(2)解:甲的平均成绩为$\frac{10 + 8 + 9 + 10 + 8}{5} = \frac{45}{5} = 9$(环)
因为甲、乙平均值相等,所以乙的平均成绩也为9环,即$\frac{10 + 9 + 9 + a + b}{5} = 9$
解得$10 + 9 + 9 + a + b = 45$,$a + b = 17$
(3)解:甲成绩的方差$s^{2}_{甲}=\frac{1}{5}[(10 - 9)^{2}+(8 - 9)^{2}+(9 - 9)^{2}+(10 - 9)^{2}+(8 - 9)^{2}]=\frac{1}{5}(1 + 1 + 0 + 1 + 1)=\frac{4}{5}=0.8$
乙成绩的方差$s^{2}_{乙}=\frac{1}{5}[(10 - 9)^{2}+(9 - 9)^{2}+(9 - 9)^{2}+(a - 9)^{2}+(b - 9)^{2}]=\frac{1}{5}[1 + 0 + 0 + (a - 9)^{2}+(b - 9)^{2}]$
因为$a + b = 17$,所以$b = 17 - a$,代入得$s^{2}_{乙}=\frac{1}{5}[1 + (a - 9)^{2}+(8 - a)^{2}]$
要使乙比甲稳定,则$s^{2}_{乙}<0.8$,即$(a - 9)^{2}+(8 - a)^{2}<3$
整数解为$a = 8$,$b = 9$或$a = 9$,$b = 8$
答案:(2)17;(3)$a=8$,$b=9$;$a=9$,$b=8$
查看更多完整答案,请扫码查看


