2025年新编高中同步作业高中数学选择性必修第一册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第一册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
任务三 椭圆的离心率
[探究活动]
“天宫一号”的运行轨迹是椭圆形的,椭圆在我们的生活中经常出现.
探究1:若椭圆的一个顶点与两个焦点构成等边三角形,则椭圆的离心率为( )
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{3}}{4}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{1}{2}$
探究2:已知椭圆$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$(a>b>0),A是左顶点,F是右焦点,B是短轴的一个顶点,∠ABF = 90°,则称其为“优美椭圆”. 它的离心率e = ______.
[探究活动]
“天宫一号”的运行轨迹是椭圆形的,椭圆在我们的生活中经常出现.

探究1:若椭圆的一个顶点与两个焦点构成等边三角形,则椭圆的离心率为( )
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{3}}{4}$
C. $\frac{\sqrt{3}}{3}$
D. $\frac{1}{2}$
探究2:已知椭圆$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$(a>b>0),A是左顶点,F是右焦点,B是短轴的一个顶点,∠ABF = 90°,则称其为“优美椭圆”. 它的离心率e = ______.
答案:
[探究活动]
探究1 D 提示:如图,椭圆的短轴的一个端点与焦点构成等边三角形,则$\angle BF_{1}F_{2}=60^{\circ}$,$\tan\angle BF_{1}F_{2}=\frac{|OB|}{|OF_{1}|}=\frac{b}{c}=\sqrt{3}$,所以$b=\sqrt{3}c$. 又$a^{2}=b^{2}+c^{2}=3c^{2}+c^{2}=4c^{2}$,所以$e=\frac{c}{a}=\frac{1}{2}$. 故选D.
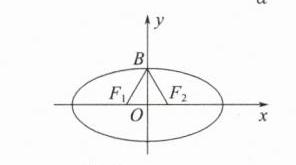
探究2 $\frac{-1+\sqrt{5}}{2}$ 提示:如图所示,由题意知,$|AO| = a$,$|OF| = c$,$|BF| = a$,$|AB|=\sqrt{a^{2}+b^{2}}$,$a^{2}=b^{2}+c^{2}$,所以在直角三角形$ABF$中,$a^{2}+b^{2}+a^{2}=(a + c)^{2}=a^{2}+2ac + c^{2}$,即$a^{2}-c^{2}-ac = 0$,两边同除以$a^{2}$,得$e^{2}+e - 1 = 0$,解得$e=\frac{-1+\sqrt{5}}{2}$或$e=\frac{-1-\sqrt{5}}{2}$(舍去).
[探究活动]
探究1 D 提示:如图,椭圆的短轴的一个端点与焦点构成等边三角形,则$\angle BF_{1}F_{2}=60^{\circ}$,$\tan\angle BF_{1}F_{2}=\frac{|OB|}{|OF_{1}|}=\frac{b}{c}=\sqrt{3}$,所以$b=\sqrt{3}c$. 又$a^{2}=b^{2}+c^{2}=3c^{2}+c^{2}=4c^{2}$,所以$e=\frac{c}{a}=\frac{1}{2}$. 故选D.

探究2 $\frac{-1+\sqrt{5}}{2}$ 提示:如图所示,由题意知,$|AO| = a$,$|OF| = c$,$|BF| = a$,$|AB|=\sqrt{a^{2}+b^{2}}$,$a^{2}=b^{2}+c^{2}$,所以在直角三角形$ABF$中,$a^{2}+b^{2}+a^{2}=(a + c)^{2}=a^{2}+2ac + c^{2}$,即$a^{2}-c^{2}-ac = 0$,两边同除以$a^{2}$,得$e^{2}+e - 1 = 0$,解得$e=\frac{-1+\sqrt{5}}{2}$或$e=\frac{-1-\sqrt{5}}{2}$(舍去).
[评价活动]
1.(2024·九省联考)椭圆$\frac{x^{2}}{a^{2}}+y^{2}=1$(a>1)的离心率为$\frac{1}{2}$,则a = ( )
A. $\frac{2\sqrt{3}}{3}$
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
1.(2024·九省联考)椭圆$\frac{x^{2}}{a^{2}}+y^{2}=1$(a>1)的离心率为$\frac{1}{2}$,则a = ( )
A. $\frac{2\sqrt{3}}{3}$
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2
答案:
[评价活动]
1. A 解析:由题意,得$e=\frac{\sqrt{a^{2}-1}}{a}=\frac{1}{2}$,解得$a=\frac{2\sqrt{3}}{3}$. 故选A.
1. A 解析:由题意,得$e=\frac{\sqrt{a^{2}-1}}{a}=\frac{1}{2}$,解得$a=\frac{2\sqrt{3}}{3}$. 故选A.
2.(2022·全国甲卷(理))椭圆C:$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$(a>b>0)的左顶点为A,点P,Q均在C上,且关于y轴对称. 若直线AP,AQ的斜率之积为$\frac{1}{4}$,则椭圆C的离心率为( )
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{2}$
D. $\frac{1}{3}$
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{2}$
D. $\frac{1}{3}$
答案:
2. A 解析:设$P(x_{1},y_{1})$,则$Q(-x_{1},y_{1})$.
由$k_{AP}\cdot k_{AQ}=\frac{1}{4}$,得$k_{AP}\cdot k_{AQ}=\frac{y_{1}}{x_{1}+a}\cdot\frac{y_{1}}{-x_{1}+a}=\frac{y_{1}^{2}}{-x_{1}^{2}+a^{2}}=\frac{1}{4}$. 由$\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{b^{2}}=1$,得$y_{1}^{2}=\frac{b^{2}(a^{2}-x_{1}^{2})}{a^{2}}$,所以$\frac{\frac{b^{2}(a^{2}-x_{1}^{2})}{a^{2}}}{-x_{1}^{2}+a^{2}}=\frac{1}{4}$,即$\frac{b^{2}}{a^{2}}=\frac{1}{4}$,所以椭圆$C$的离心率$e=\frac{c}{a}=\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{\sqrt{3}}{2}$. 故选A.
由$k_{AP}\cdot k_{AQ}=\frac{1}{4}$,得$k_{AP}\cdot k_{AQ}=\frac{y_{1}}{x_{1}+a}\cdot\frac{y_{1}}{-x_{1}+a}=\frac{y_{1}^{2}}{-x_{1}^{2}+a^{2}}=\frac{1}{4}$. 由$\frac{x_{1}^{2}}{a^{2}}+\frac{y_{1}^{2}}{b^{2}}=1$,得$y_{1}^{2}=\frac{b^{2}(a^{2}-x_{1}^{2})}{a^{2}}$,所以$\frac{\frac{b^{2}(a^{2}-x_{1}^{2})}{a^{2}}}{-x_{1}^{2}+a^{2}}=\frac{1}{4}$,即$\frac{b^{2}}{a^{2}}=\frac{1}{4}$,所以椭圆$C$的离心率$e=\frac{c}{a}=\sqrt{1-\frac{b^{2}}{a^{2}}}=\frac{\sqrt{3}}{2}$. 故选A.
查看更多完整答案,请扫码查看


