2025年新编高中同步作业高中数学选择性必修第一册人教版A
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新编高中同步作业高中数学选择性必修第一册人教版A 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
任务二 求二面角
1. 如图,$PA\perp$平面$ABC$,$AC\perp BC$,$PA = AC = 1$,$BC = \sqrt{2}$,则平面$APB$与平面$PBC$的夹角的余弦值为______.
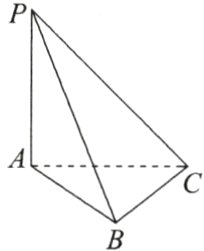
1. 如图,$PA\perp$平面$ABC$,$AC\perp BC$,$PA = AC = 1$,$BC = \sqrt{2}$,则平面$APB$与平面$PBC$的夹角的余弦值为______.

答案:
$\frac{\sqrt{3}}{3}$ 解析:如图,建立空间直角坐标系Axyz,
则A(0,0,0),B($\sqrt{2}$,1,0),C(0,1,0),P(0,0,1),
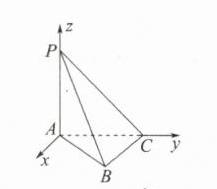
所以$\overrightarrow{AP}=(0,0,1)$,$\overrightarrow{AB}=(\sqrt{2},1,0)$,$\overrightarrow{CB}=(\sqrt{2},0,0)$,$\overrightarrow{CP}=(0,-1,1)$.
设平面PAB的法向量为$\boldsymbol{m}=(x,y,z)$,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AP} = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AB} = 0\end{cases}$,
即$\begin{cases}(x,y,z)\cdot(0,0,1) = 0 \\ (x,y,z)\cdot(\sqrt{2},1,0) = 0\end{cases}$,解得$\begin{cases}y = -\sqrt{2}x \\ z = 0\end{cases}$,
令x = 1,得$\boldsymbol{m}=(1,-\sqrt{2},0)$为平面PAB的一个法向量.
设平面PBC的法向量为$\boldsymbol{n}=(x',y',z')$,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{CB} = 0 \\ \boldsymbol{n}\cdot\overrightarrow{CP} = 0\end{cases}$,
即$\begin{cases}(x',y',z')\cdot(\sqrt{2},0,0) = 0 \\ (x',y',z')\cdot(0,-1,1) = 0\end{cases}$,解得$\begin{cases}x' = 0 \\ y' = z'\end{cases}$,
令y' = -1,得$\boldsymbol{n}=(0,-1,-1)$为平面PBC的一个法向量,
所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle = \frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}|\cdot|\boldsymbol{n}|} = \frac{\sqrt{3}}{3}$.
设平面APB与平面PBC的夹角为θ,
则$\cos\theta = |\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle| = \frac{\sqrt{3}}{3}$,即平面APB与平面PBC的夹角的余弦值为$\frac{\sqrt{3}}{3}$.
$\frac{\sqrt{3}}{3}$ 解析:如图,建立空间直角坐标系Axyz,
则A(0,0,0),B($\sqrt{2}$,1,0),C(0,1,0),P(0,0,1),

所以$\overrightarrow{AP}=(0,0,1)$,$\overrightarrow{AB}=(\sqrt{2},1,0)$,$\overrightarrow{CB}=(\sqrt{2},0,0)$,$\overrightarrow{CP}=(0,-1,1)$.
设平面PAB的法向量为$\boldsymbol{m}=(x,y,z)$,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AP} = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AB} = 0\end{cases}$,
即$\begin{cases}(x,y,z)\cdot(0,0,1) = 0 \\ (x,y,z)\cdot(\sqrt{2},1,0) = 0\end{cases}$,解得$\begin{cases}y = -\sqrt{2}x \\ z = 0\end{cases}$,
令x = 1,得$\boldsymbol{m}=(1,-\sqrt{2},0)$为平面PAB的一个法向量.
设平面PBC的法向量为$\boldsymbol{n}=(x',y',z')$,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{CB} = 0 \\ \boldsymbol{n}\cdot\overrightarrow{CP} = 0\end{cases}$,
即$\begin{cases}(x',y',z')\cdot(\sqrt{2},0,0) = 0 \\ (x',y',z')\cdot(0,-1,1) = 0\end{cases}$,解得$\begin{cases}x' = 0 \\ y' = z'\end{cases}$,
令y' = -1,得$\boldsymbol{n}=(0,-1,-1)$为平面PBC的一个法向量,
所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle = \frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}|\cdot|\boldsymbol{n}|} = \frac{\sqrt{3}}{3}$.
设平面APB与平面PBC的夹角为θ,
则$\cos\theta = |\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle| = \frac{\sqrt{3}}{3}$,即平面APB与平面PBC的夹角的余弦值为$\frac{\sqrt{3}}{3}$.
2. 如图,几何体是圆柱的一部分,它是由矩形$ABCD$(及其内部)以$AB$边所在直线为旋转轴旋转$120^{\circ}$得到的,$G$是$\overset{\frown}{DF}$的中点.
(1)设$P$是$\overset{\frown}{CE}$上的一点,且$AP\perp BE$,求$\angle CBP$的大小;
(2)当$AB = 3$,$AD = 2$时,求平面$AEG$与平面$ACG$的夹角的大小.
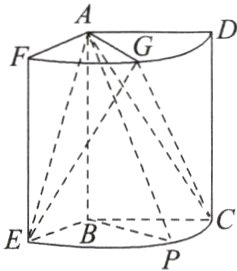
(1)设$P$是$\overset{\frown}{CE}$上的一点,且$AP\perp BE$,求$\angle CBP$的大小;
(2)当$AB = 3$,$AD = 2$时,求平面$AEG$与平面$ACG$的夹角的大小.

答案:
解:
(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP = A,
所以BE⊥平面ABP.
又BP⊂平面ABP,
所以BE⊥BP.
又∠EBC = 120°,
所以∠CBP = 30°.
(2)以B为坐标原点,分别以BE,BP,BA所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.

由题意,得A(0,0,3),E(2,0,0),G(1,$\sqrt{3}$,3),C(-1,$\sqrt{3}$,0),
故$\overrightarrow{AE}=(2,0,-3)$,$\overrightarrow{AG}=(1,\sqrt{3},0)$,$\overrightarrow{CG}=(2,0,3)$.
设$\boldsymbol{m}=(x_1,y_1,z_1)$是平面AEG的法向量,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE} = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AG} = 0\end{cases}$,即$\begin{cases}2x_1 - 3z_1 = 0 \\ x_1 + \sqrt{3}y_1 = 0\end{cases}$,
取z_1 = 2,可得平面AEG的一个法向量$\boldsymbol{m}=(3,-\sqrt{3},2)$.
设$\boldsymbol{n}=(x_2,y_2,z_2)$是平面ACG的法向量,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AG} = 0 \\ \boldsymbol{n}\cdot\overrightarrow{CG} = 0\end{cases}$,即$\begin{cases}x_2 + \sqrt{3}y_2 = 0 \\ 2x_2 + 3z_2 = 0\end{cases}$,
取z_2 = -2,可得平面ACG的一个法向量$\boldsymbol{n}=(3,-\sqrt{3},-2)$,
所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle = \frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}|\cdot|\boldsymbol{n}|} = \frac{1}{2}$.
设平面AEG与平面ACG的夹角为θ,
则$\cos\theta = |\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle| = \frac{1}{2}$,
所以平面AEG与平面ACG的夹角的大小为60°.
解:
(1)因为AP⊥BE,AB⊥BE,AB,AP⊂平面ABP,AB∩AP = A,
所以BE⊥平面ABP.
又BP⊂平面ABP,
所以BE⊥BP.
又∠EBC = 120°,
所以∠CBP = 30°.
(2)以B为坐标原点,分别以BE,BP,BA所在的直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.

由题意,得A(0,0,3),E(2,0,0),G(1,$\sqrt{3}$,3),C(-1,$\sqrt{3}$,0),
故$\overrightarrow{AE}=(2,0,-3)$,$\overrightarrow{AG}=(1,\sqrt{3},0)$,$\overrightarrow{CG}=(2,0,3)$.
设$\boldsymbol{m}=(x_1,y_1,z_1)$是平面AEG的法向量,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE} = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AG} = 0\end{cases}$,即$\begin{cases}2x_1 - 3z_1 = 0 \\ x_1 + \sqrt{3}y_1 = 0\end{cases}$,
取z_1 = 2,可得平面AEG的一个法向量$\boldsymbol{m}=(3,-\sqrt{3},2)$.
设$\boldsymbol{n}=(x_2,y_2,z_2)$是平面ACG的法向量,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AG} = 0 \\ \boldsymbol{n}\cdot\overrightarrow{CG} = 0\end{cases}$,即$\begin{cases}x_2 + \sqrt{3}y_2 = 0 \\ 2x_2 + 3z_2 = 0\end{cases}$,
取z_2 = -2,可得平面ACG的一个法向量$\boldsymbol{n}=(3,-\sqrt{3},-2)$,
所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle = \frac{\boldsymbol{m}\cdot\boldsymbol{n}}{|\boldsymbol{m}|\cdot|\boldsymbol{n}|} = \frac{1}{2}$.
设平面AEG与平面ACG的夹角为θ,
则$\cos\theta = |\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle| = \frac{1}{2}$,
所以平面AEG与平面ACG的夹角的大小为60°.
3. (2022·新高考全国Ⅱ卷)如图,$PO$是三棱锥$P - ABC$的高,$PA = PB$,$AB\perp AC$,$E$是$PB$的中点.
(1)证明:$OE//$平面$PAC$;
(2)若$\angle ABO = \angle CBO = 30^{\circ}$,$PO = 3$,$PA = 5$,求二面角$C - AE - B$的正弦值.
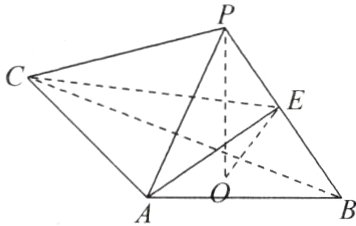
(1)证明:$OE//$平面$PAC$;
(2)若$\angle ABO = \angle CBO = 30^{\circ}$,$PO = 3$,$PA = 5$,求二面角$C - AE - B$的正弦值.

答案:
(1)证明:如图,连接BO并延长交AC于点D,连接OA,PD.
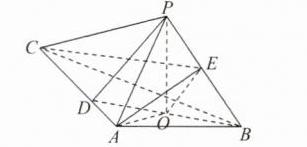
因为PO是三棱锥P - ABC的高,
所以PO⊥平面ABC,AO,BO⊂平面ABC,
所以PO⊥AO,PO⊥BO.
又PA = PB,
所以△POA≌△POB,即OA = OB,
所以∠OAB = ∠OBA.
又AB⊥AC,即∠BAC = 90°,
所以∠OAB + ∠OAD = 90°,∠OBA + ∠ODA = 90°,
所以∠ODA = ∠OAD,
所以AO = DO,即AO = DO = OB,
所以O为BD的中点.
又E为PB的中点,
所以OE//PD.
因为OE⊄平面PAC,PD⊂平面PAC,
所以OE//平面PAC.
(2)解:过点A作Az//OP,建立如图所示的空间直角坐标系.
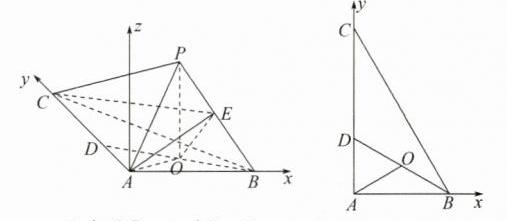
因为PO = 3,AP = 5,
所以OA = $\sqrt{AP^2 - PO^2} = 4$,
又∠OBA = ∠OBC = 30°,
所以BD = 2OA = 8,
所以AD = 4,AB = 4$\sqrt{3}$,
所以AC = 12,
所以A(0,0,0),O(2$\sqrt{3}$,2,0),B(4$\sqrt{3}$,0,0),P(2$\sqrt{3}$,2,3),C(0,12,0),E(3$\sqrt{3}$,1,$\frac{3}{2}$),
所以$\overrightarrow{AE}=(3\sqrt{3},1,\frac{3}{2})$,$\overrightarrow{AB}=(4\sqrt{3},0,0)$,$\overrightarrow{AC}=(0,12,0)$.
设平面AEB的法向量为$\boldsymbol{n}=(x,y,z)$,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AE} = 3\sqrt{3}x + y + \frac{3}{2}z = 0 \\ \boldsymbol{n}\cdot\overrightarrow{AB} = 4\sqrt{3}x = 0\end{cases}$,
令z = 2,则y = -3,x = 0,
所以$\boldsymbol{n}=(0,-3,2)$.
设平面AEC的法向量为$\boldsymbol{m}=(a,b,c)$,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE} = 3\sqrt{3}a + b + \frac{3}{2}c = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AC} = 12b = 0\end{cases}$,
令a = $\sqrt{3}$,则c = -6,b = 0,
所以$\boldsymbol{m}=(\sqrt{3},0,-6)$,
所以$\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle = \frac{\boldsymbol{n}\cdot\boldsymbol{m}}{|\boldsymbol{n}|\cdot|\boldsymbol{m}|} = \frac{-12}{\sqrt{13}\times\sqrt{39}} = -\frac{4\sqrt{3}}{13}$.
设二面角C - AE - B的大小为θ,
则$|\cos\theta| = |\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle| = \frac{4\sqrt{3}}{13}$,
所以$\sin\theta = \sqrt{1 - \cos^2\theta} = \frac{11}{13}$,即二面角C - AE - B的正弦值为$\frac{11}{13}$.
(1)证明:如图,连接BO并延长交AC于点D,连接OA,PD.

因为PO是三棱锥P - ABC的高,
所以PO⊥平面ABC,AO,BO⊂平面ABC,
所以PO⊥AO,PO⊥BO.
又PA = PB,
所以△POA≌△POB,即OA = OB,
所以∠OAB = ∠OBA.
又AB⊥AC,即∠BAC = 90°,
所以∠OAB + ∠OAD = 90°,∠OBA + ∠ODA = 90°,
所以∠ODA = ∠OAD,
所以AO = DO,即AO = DO = OB,
所以O为BD的中点.
又E为PB的中点,
所以OE//PD.
因为OE⊄平面PAC,PD⊂平面PAC,
所以OE//平面PAC.
(2)解:过点A作Az//OP,建立如图所示的空间直角坐标系.

因为PO = 3,AP = 5,
所以OA = $\sqrt{AP^2 - PO^2} = 4$,
又∠OBA = ∠OBC = 30°,
所以BD = 2OA = 8,
所以AD = 4,AB = 4$\sqrt{3}$,
所以AC = 12,
所以A(0,0,0),O(2$\sqrt{3}$,2,0),B(4$\sqrt{3}$,0,0),P(2$\sqrt{3}$,2,3),C(0,12,0),E(3$\sqrt{3}$,1,$\frac{3}{2}$),
所以$\overrightarrow{AE}=(3\sqrt{3},1,\frac{3}{2})$,$\overrightarrow{AB}=(4\sqrt{3},0,0)$,$\overrightarrow{AC}=(0,12,0)$.
设平面AEB的法向量为$\boldsymbol{n}=(x,y,z)$,
则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{AE} = 3\sqrt{3}x + y + \frac{3}{2}z = 0 \\ \boldsymbol{n}\cdot\overrightarrow{AB} = 4\sqrt{3}x = 0\end{cases}$,
令z = 2,则y = -3,x = 0,
所以$\boldsymbol{n}=(0,-3,2)$.
设平面AEC的法向量为$\boldsymbol{m}=(a,b,c)$,
则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AE} = 3\sqrt{3}a + b + \frac{3}{2}c = 0 \\ \boldsymbol{m}\cdot\overrightarrow{AC} = 12b = 0\end{cases}$,
令a = $\sqrt{3}$,则c = -6,b = 0,
所以$\boldsymbol{m}=(\sqrt{3},0,-6)$,
所以$\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle = \frac{\boldsymbol{n}\cdot\boldsymbol{m}}{|\boldsymbol{n}|\cdot|\boldsymbol{m}|} = \frac{-12}{\sqrt{13}\times\sqrt{39}} = -\frac{4\sqrt{3}}{13}$.
设二面角C - AE - B的大小为θ,
则$|\cos\theta| = |\cos\langle\boldsymbol{n},\boldsymbol{m}\rangle| = \frac{4\sqrt{3}}{13}$,
所以$\sin\theta = \sqrt{1 - \cos^2\theta} = \frac{11}{13}$,即二面角C - AE - B的正弦值为$\frac{11}{13}$.
查看更多完整答案,请扫码查看


