《2025年新编高中同步作业高中数学选择性必修第一册人教版A》

任务一 直线的倾斜角
1. 下列说法中，正确的是 （ ）
A. 若直线的倾斜角为α，则此直线的斜率为tanα
B. 若直线的斜率为tanα，则此直线的倾斜角为α
C. 若直线的倾斜角为α，则tanα＞0
D. 任意直线都有倾斜角，但它不一定有斜率

答案： D 解析：当$\alpha = 90^{\circ}$时，直线的斜率不存在，故A错误；直线斜率为$\tan\alpha$，但只有$0^{\circ}\leq\alpha＜180^{\circ}$时，$\alpha$才是直线的倾斜角，故B错误；$\alpha = 0^{\circ}$时，$\tan\alpha = 0$，故C错误；D正确. 故选D.

2. 一条直线l与x轴相交，其向上方向与y轴正方向所成的角为α(0°＜α＜90°)，则其倾斜角为 （ ）
A. α
B. 180°-α
C. 180°-α或90°-α
D. 90°+α或90°-α

答案： D 解析：如图，当$l$向上方向的部分在$y$轴左侧时，倾斜角为$90^{\circ}+\alpha$；当$l$向上方向的部分在$y$轴右侧时，倾斜角为$90^{\circ}-\alpha$. 故选D.

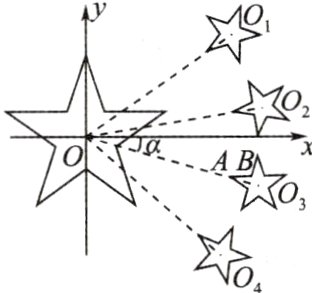
3. 1949年公布的《国旗制法说明》中就五星的位置规定：大五角星有一个角尖正向上方，四颗小五角星均各有一个角尖正对大五角星的中心点. 有人发现，第三颗小星的姿态与大星相近. 为便于研究，如图，以大星的中心点为原点，建立直角坐标系，OO₁，OO₂，OO₃，OO₄分别是大星中心点与四颗小星中心点的连接线，α≈16°，则第三颗小星的一条边AB所在直线的倾斜角约为 （ ）
　　　　　　
　
A. 0°　　
　B. 1°　　
　C. 2°　　
　D. 3°

答案： C 解析：因为$O,O_{3}$都为五角星的中心点，所以$OO_{3}$平分第三颗小星的一个角. 由五角星的内角为$36^{\circ}$知，$\angle BAO_{3}=18^{\circ}$，过$O_{3}$作$x$轴的平行线$O_{3}E$，如下图，则$\angle OO_{3}E=\alpha\approx16^{\circ}$，所以直线$AB$的倾斜角为$18^{\circ}-16^{\circ}=2^{\circ}$.

任务二 直线的斜率
1. 已知点A的坐标为(3,4)，在坐标轴上有一点B. 若kₐₙ=4，则点B的坐标为 （ ）
A. (2,0)或(0,-4)
B. (2,0)或(0,-8)
C. (2,0)
D. (0,-8)

答案： B 解析：设$B(x,0)$或$(0,y)$. 因为$k_{AB}=\frac{4}{3 - x}$或$k_{AB}=\frac{4 - y}{3}$，所以$\frac{4}{3 - x}=4$或$\frac{4 - y}{3}=4$，所以$x = 2$，$y = - 8$，所以点$B$的坐标为$(2,0)$或$(0,-8)$.

2. 已知直线AB与直线AC有相同的斜率，且A(1,0)，B(2,a)，C(a,1)，则实数a的值是______.

答案： $\frac{1\pm\sqrt{5}}{2}$ 解析：依题意，得$k_{AB}=k_{AC}$，即$\frac{a - 0}{2 - 1}=\frac{1 - 0}{a - 1}$，解得$a=\frac{1\pm\sqrt{5}}{2}$.

3. 经过A(1,5)，B(3,2)两点的直线的方向向量为(2,k)，则实数k=______.

答案： - 3 解析：由题意可知，直线的方向向量为$\overrightarrow{AB}=(3 - 1,2 - 5)=(2,-3)$，故$k=-3$.

任务三 直线斜率的应用

[探究活动]
　　探究1:观察如图所示的直线l₁，l₂，l₃，l₄.
　　　　　
　　(1)直线l₁，l₂，l₃，l₄的倾斜角发生什么变化?
　　
(2)直线l₁，l₂，l₃，l₄的斜率发生了什么变化?
　探究2:过点M(0,−3)的直线l与以点
A(3,0)，B(−4,1)为端点的线段AB有公共点，求直线l的斜率k的取值范围.

答案： 探究1 提示：
(1)倾斜角逐渐增大.
(2)从$l_{1}$到$l_{2}$斜率为正，逐渐变大，从$l_{3}$到$l_{4}$斜率为负，逐渐变大.
探究2 提示：由题意与斜率公式可知，直线$AM$与$BM$的斜率分别为$k_{AM}=\frac{0 - (-3)}{3 - 0}=1$，$k_{BM}=\frac{1 - (-3)}{-4 - 0}=-1$. 如图所示，
直线$l$相当于绕点$M$在直线$AM$与$BM$间旋转. 当$l$由$AM$位置旋转到$y$轴位置时，倾斜角增大到$90^{\circ}$，又$k_{AM}=1$，所以$k\geq1$；当$l$从$y$轴位置旋转到$BM$位置时，倾斜角大于$90^{\circ}$，又$k_{BM}=-1$，所以$k\leq - 1$. 综上所述，直线$l$的斜率$k$的取值范围是$(-\infty,-1]\cup[1,+\infty)$.