《2025年一线调研学业测评七年级数学下册北师大版》

1. 如图，已知△ABC的三条边、三个角，则甲、乙两个三角形中，与△ABC全等的图形是（ ）

A. 甲
B. 乙
C. 甲和乙
D. 都不是

答案： A

2. [教材P109习题T15变式]如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）


A. SSS
B. SAS
C. AAS
D. ASA

答案： D

3. 如图，已知∠1 = ∠2，要根据“ASA”判定△ABD≌△ACD，则需要补充的一个条件为______________。

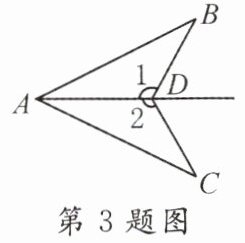
答案： $\angle BAD = \angle CAD$

4. 如图，在△ABC和△DCE中，AB = CD，∠B = ∠DCE = 90°，点A，C，D依次在同一直线上，且AB//DE。试说明△ABC≌△DCE。

答案： 解：因为$AB// DE$，所以$\angle BAC = \angle D$。又因为$\angle B = \angle DCE = 90^{\circ},AB = CD$，所以$\triangle ABC\cong\triangle DCE(ASA)$。

5. 如图，在△ACD中，∠CAD = 90°，AC = 8，AD = 10，AB//CD，E是CD上一点，BE交AD于点F，若点F是AD的中点时，则图中阴影部分的面积为（ ）


A. 10
B. 20
C. 40
D. 80

答案： C

6. 如图，点P在∠AOB的平分线上，PE⊥OA于E，PF⊥OB于F，若PE = 3，则PF = ______。

答案： 3

7. 如图，在四边形ABCD中，∠ABC = 90°，AD//BC，以B为圆心，BC的长为半径画弧，与AD交于点E，连接BE，过点C作CF⊥BE，垂足为F。若AE = 8，BC = 10，则EF的长为______。

答案： 2

8. 如图，AB//CD，E，F分别为AB，CD上的点，且EC//BF，连接AD，分别与EC，BF交于点G，H，若AB = CD，试说明AG = DH。

答案： 解：因为$AB// CD$，所以$\angle A = \angle D$，因为$EC// BF$，所以$\angle AHB = \angle DGC$。又因为$AB = DC$，所以$\triangle ABH\cong\triangle DCG(AAS)$。所以$AH = DG$。所以$AH - GH = DG - GH$，即$AG = DH$。