《2025年一线调研学业测评七年级数学下册北师大版》

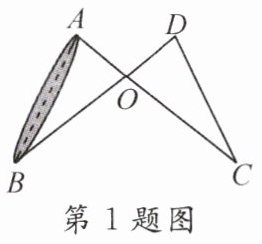
1. 如图，要测量池塘两岸相对的两点A，B间的距离，作线段AC与BD相交于点O，使AC = BD，AO = DO，只要测得C，D之间的距离，就可知道A，B间的距离，此方案依据的数学定理或基本事实是（ ）


A. ASA
B. SAS
C. SSS
D. AAS

答案： B

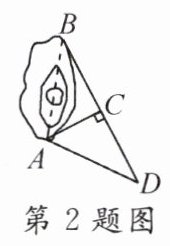
2. 如图，为了测量A，B两点之间的距离，在地面上找到一点C，连接BC，AC，使∠ACB = 90°，然后在BC的延长线上确定点D，使CD = BC，那么只需测量出的长度是（ ）


A. CD
B. AD
C. AC
D. BC

答案： B

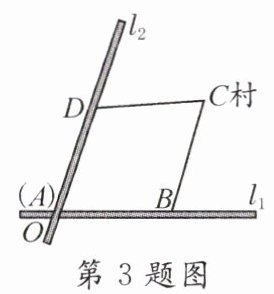
3. 如图，两条笔直的公路l₁，l₂相交于点O，公路的旁边建了三个加工厂A，B，D，已知AB = AD = 5.2km，CB = CD = 5km，C村到公路l₁的距离为4km，则C村到公路l₂的距离是（ ）


A. 3km
B. 4km
C. 5km
D. 5.2km

答案：
B 【解析】如图，连接$AC$，过点$C$作$CE\perp l_{2}$于点$E$，作$CF\perp l_{1}$于点$F$。由$AD = AB$，$DC = BC$，$AC = AC$，得$\triangle ADC\cong\triangle ABC$，所以$\angle DAC=\angle BAC$。又因为$\angle AEC=\angle AFC = 90^{\circ}$，$AC = AC$，所以$\triangle AEC\cong\triangle AFC$。所以$CE = CF = 4\text{km}$，即$C$村到公路$l_{2}$的距离是$4\text{km}$。

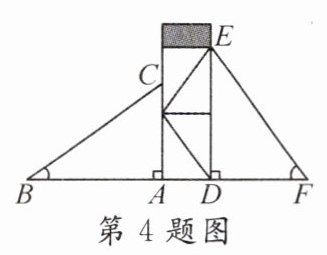
4. 如图，有两个滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，左边滑梯水平方向的长度AB与右边滑梯的高度DE相等，测得BC = 2.5m，则EF = ______m。

答案： 2.5

5. 如图所示，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD = 1km，DC = 1km，村庄A，C间和A，D间也有公路相连，且公路AD是南北走向，AC = 3km，只有村庄A，B之间由于隔了一个小湖，所以无直接相连的公路。现决定在湖面上造一座斜拉桥，测得AE = 1.2km，BF = 0.7km，则建造的斜拉桥长至少有______km。

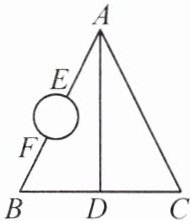
答案： 1.1

6. 在学习“利用三角形全等测距离”之后，张老师给同学们布置作业，测量校内池塘A，B之间的距离（无法直接测量）。
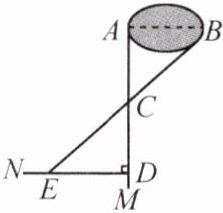
小颖设计的方案是：先过点A作AB的垂线AM，在AM上顺次截取AC，CD，使CD = AC，然后过点D作DN⊥AD，连接BC并延长交DN于点E，则DE的长度即为AB的长度。
（1）小颖的作法你同意吗？并说明理由；
（2）如果利用全等三角形去解决这个问题，请你设计一个与小颖的全等依据不同的方案，并画出图形。

答案：
解:
(1)同意。理由:在$\triangle ABC$和$\triangle DEC$中，因为$\angle BAC=\angle EDC$，$AC = DC$，$\angle ACB=\angle DCE$，所以$\triangle ABC\cong\triangle DEC(\text{ASA})$。所以$AB = DE$，所以$DE$的长度即为$AB$的长度。
(2)如图，取一点$O$，使得能从点$O$直接到达点$A$，$B$，连接$AO$，$BO$，分别延长$AO$，$BO$到点$D$，$E$，使得$OD = OA$，$OE = OB$，则$DE$的长度即为$AB$的长度。