《2025年一线调研学业测评七年级数学下册北师大版》

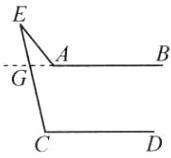
1. 如图1，木杆AB与CD平行，木杆的两端A，C用一条橡皮筋连接，点E是橡皮筋上的一点。
(1)观察发现：在图1中，则∠A，∠C与∠AEC之间的数量关系是______________。
(2)拓展探究：若将橡皮筋拉成如图2的形状，则∠A，∠C与∠AEC之间的数量关系是____________________。
(3)类比探究：若将橡皮筋拉成如图3的形状，类比(2)中的方法探究∠AEC，∠EAB与∠ECD之间有何关系？并说明理由。

答案：
解:
(1)∠A + ∠C = ∠AEC　
(2)∠AEC = ∠A + ∠C
(3)∠EAB = ∠AEC + ∠ECD,理由如下:
如图，延长BA交CE于G，
因为AB // CD,
所以∠EGB = ∠C,
因为∠EAB = 180°−∠EAG，∠AEC + ∠EGB = 180°−∠EAG，所以∠EAB = ∠AEC + ∠EGB,
所以∠EAB = ∠AEC + ∠ECD。

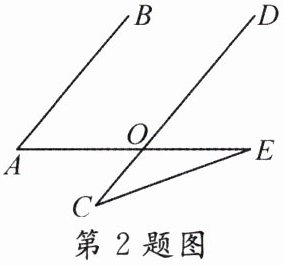
2. 如图，AB//CD，∠C = 30°，∠E = 20°，则∠A的度数是（ ）


A. 10°
B. 50°
C. 40°
D. 45°

答案： B

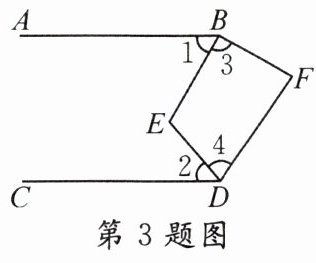
3. 如图所示，AB//CD，若∠3 = $\frac{3}{2}$∠1，∠4 = $\frac{3}{2}$∠2，下列各式：①∠1 + ∠2 = ∠E；②∠1 + ∠2 + ∠3 + ∠4 = ∠F；③∠3 + ∠4 + ∠F = 360°；④5∠E + 2∠F = 720°，其中正确的是（ ）


A. ①②
B. ①③
C. ②③
D. ①④

答案： D

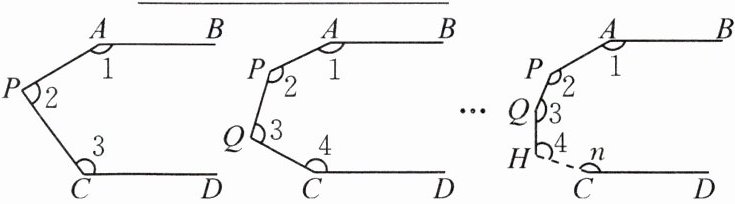
4. 如图，已知AB//CD，易得∠1 + ∠2 + ∠3 = 360°，∠1 + ∠2 + ∠3 + ∠4 = ________，……根据以上的规律得∠1 + ∠2 + ∠3 + … + ∠n = ______________。

答案： 540°　(n - 1)·180°

5. 如图，若直线l₁//l₂，∠α = ∠β，∠1 = 40°，则∠2的度数为______。

答案： 140°

6. (1)如图1，AB//CD，则∠E + ∠G与∠B + ∠F + ∠D有什么样的数量关系？
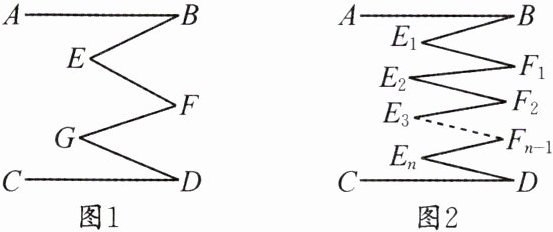
(2)如图2，若AB//CD，则能得到什么结论？请直接写出结论。

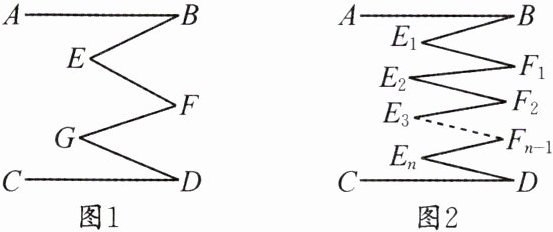
答案：
解:
(1)如图，过点E作EM // AB，过点F作FN // AB，过点G作GH // CD,

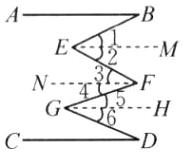
因为AB // CD,
所以AB // EM // FN // GH,
所以∠1 = ∠B，∠2 = ∠3，∠4 = ∠5，∠6 = ∠D,
所以∠1 + ∠2 + ∠5 + ∠6 = ∠B + ∠3 + ∠4 + ∠D,
即∠BEF + ∠FGD = ∠B + ∠EFG + ∠D。
(2)∠B + ∠F₁ + ∠F₂ + ∠Fₙ₋₁ +... + ∠D = ∠E₁ + ∠E₂ +... + ∠Eₙ。