《2025年一线调研学业测评七年级数学下册北师大版》

1. 在边长为a的正方形中挖去一个边长为b的小正方形(a＞b)(如图甲)，把余下的部分拼成一个长方形(如图乙)，根据两个图形中阴影部分的面积相等，可以验证（ ）

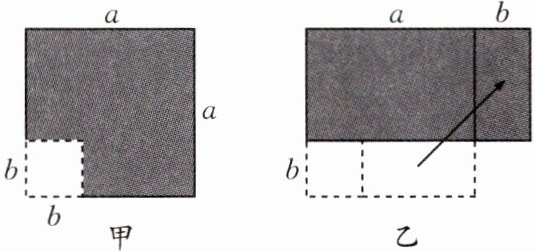
A. $a^{2}-b^{2}=(a + b)(a - b)$
B. $(a - b)^{2}=a^{2}-2ab + b^{2}$
C. $(a + b)^{2}=a^{2}+2ab + b^{2}$
D. $(a + 2b)(a - b)=a^{2}+ab - 2b^{2}$

答案： A

2. 如图，阴影部分是在边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形。给出下列2种割拼方法，其中能够验证平方差公式的是（ ）

A. 只有①
B. 只有②
C. ①②都能
D. ①②都不能

答案： C

3. 求$99\frac{2}{3}\times100\frac{1}{3}$的值时，运用简便的计算方法，可先将式子变形为（ ）
A. $(99+\frac{2}{3})(100+\frac{1}{3})$
B. $(99 + 100)(\frac{2}{3}+1)$
C. $(100\frac{1}{3}-99\frac{2}{3})^{2}$
D. $(100-\frac{1}{3})(100+\frac{1}{3})$

答案： D

4. 用平方差公式进行计算：
（1）303×297；
（2）1.01×0.99。

答案：
(1)89991
(2)0.9999

5. (赤峰中考)已知$(x + 2)(x - 2)-2x = 1$，则$2x^{2}-4x + 3$的值为（ ）
A. 13
B. 8
C. -3
D. 5

答案： A

6. 计算：
（1）$(a + b)(a - b)-a(a - b)$；
（2）$(2x - 3y)(3x + 2y)-(2x - y)(y + 2x)$。

答案：
(1)$ab - b^{2}$
(2)$2x^{2}-5xy - 5y^{2}$

7. 先运用整式乘法公式化简，再求值：$(3b - 1)(3b + 1)-(2a + 1)(2a - 1)$，其中$a = -2$，$b = 1$。

答案： 解：原式$=9b^{2}-1 - 4a^{2}+1=9b^{2}-4a^{2}$。
当$a = - 2$，$b = 1$时，原式$=9 - 16=-7$。

8. (六盘水中考)如图，学校劳动实践基地有两块边长分别为a，b的正方形秧田A，B，其中不能使用的面积为M。
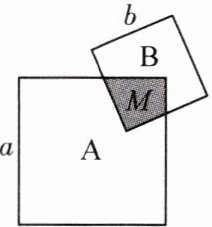
（1）用含a，M的代数式表示A中能使用的面积为__________；
（2）若$a + b = 10$，$a - b = 5$，求A比B多出的使用面积。

答案： 解：
(1)$a^{2}-M$
(2)A比B多出的使用面积为$(a^{2}-M)-(b^{2}-M)=a^{2}-b^{2}=(a + b)(a - b)=10×5 = 50$。
答：A比B多出的使用面积为50。