《2025年一线调研学业测评七年级数学下册北师大版》

1. (兰州中考)计算：$2a(a^{2}+2b)=$（ ）
A. $a^{3}+4ab$
B. $2a^{3}+2ab$
C. $2a + 4ab$
D. $2a^{3}+4ab$

答案： D

2. 一个三角形的底为$2m$，高为$m + 2n$，则它的面积为（ ）
A. $2m^{2}+4mn$
B. $m^{2}+2mn$
C. $m^{2}+4mn$
D. $2m^{2}+2mn$

答案： B

3. 若$2x(x - 2)=ax^{2}+bx$，则$a$，$b$的值为（ ）
A. $a = 1$，$b = 2$
B. $a = 2$，$b = - 2$
C. $a = 2$，$b = 4$
D. $a = 2$，$b = - 4$

答案： D

4. 图中的四边形均为长方形，根据图形，写出一个正确的等式：________________。

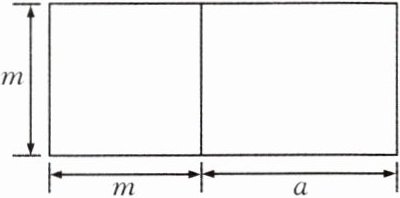
答案： $m(m + a)=m^{2}+ma$（答案不唯一）

5. 计算：
(1)$3xy(x^{2}y-\frac{1}{3}xy)$；
(2)$-3a^{2}(4a^{2}-\frac{4}{9}a + 1)$。

答案：
(1)$3x^{3}y^{2}-x^{2}y^{2}$
(2)$-12a^{4}+\frac{4}{3}a^{3}-3a^{2}$

6. 计算$(a - 2)(a + 3)$的结果是（ ）
A. $a^{2}-6$
B. $a^{2}+a - 6$
C. $a^{2}+6$
D. $a^{2}-a + 6$

答案： B

7. 若$(x + 4)(2x - 2)=2x^{2}+mx + n$，则$m$，$n$的值分别是（ ）
A. 6，8
B. - 6，- 8
C. 6，- 8
D. - 6，8

答案： C

8. 若$(3 + x)(2x^{2}+mx - 5)$的计算结果中$x^{2}$项的系数为 - 3，则$m$的值为______。

答案： -9

9. 计算：
(1)$(2m + 5)(3m - 1)$；
(2)$(-5x^{2}-7y^{2})(-2x^{2}+3y^{2})$。

答案：
(1)$6m^{2}+13m - 5$
(2)$10x^{4}-x^{2}y^{2}-21y^{4}$

10. (北京中考)已知$x^{2}+2x - 2 = 0$，求代数式$x(x + 2)+(x + 1)^{2}$的值。

答案： 解：$x(x + 2)+(x + 1)^{2}=x^{2}+2x+x^{2}+2x + 1=2x^{2}+4x + 1$。因为$x^{2}+2x - 2 = 0$，所以$x^{2}+2x = 2$。所以原式$=2(x^{2}+2x)+1=2×2 + 1=4 + 1=5$。

11. 根据图1的面积可以说明多项式的乘法运算$(2a + b)(a + b)=2a^{2}+3ab + b^{2}$，那么根据图2的面积可以说明的多项式的乘法运算是（ ）

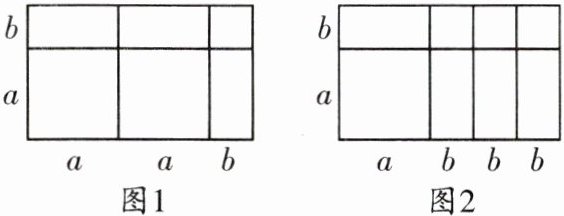
A. $(a + 3b)(a + b)=a^{2}+4ab + 3b^{2}$
B. $(a + 3b)(a + b)=a^{2}+3b^{2}$
C. $(b + 3a)(b + a)=b^{2}+4ab + 3a^{2}$
D. $(a + 3b)(a - b)=a^{2}+2ab - 3b^{2}$

答案： A