《2025年一线调研学业测评七年级数学下册北师大版》

11. 将一个长方形纸片按如图所示方式折叠，若∠1 = 40°，则∠2的度数是（ ）


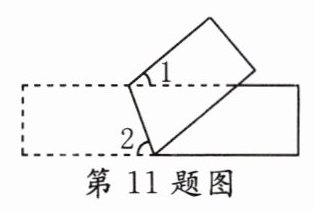
A. 40°
B. 50°
C. 60°
D. 70°

答案： D

12. (通辽中考)如图，一束光线AB先后经两平面镜OM，ON反射后，反射光线CD与AB平行，当∠ABM = 35°时，∠DCN的度数为（ ）


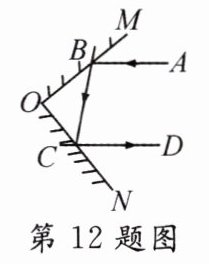
A. 55°
B. 70°
C. 60°
D. 35°

答案： A　【解析】因为$\angle ABM = 35^{\circ}$，$\angle ABM = \angle OBC$，所以$\angle OBC = 35^{\circ}$。所以$\angle ABC = 180^{\circ} - \angle ABM - \angle OBC = 180^{\circ} - 35^{\circ} - 35^{\circ} = 110^{\circ}$。因为$CD// AB$，所以$\angle ABC + \angle BCD = 180^{\circ}$。所以$\angle BCD = 180^{\circ} - \angle ABC = 70^{\circ}$。因为$\angle BCO = \angle DCN$，$\angle BCO + \angle BCD + \angle DCN = 180^{\circ}$，所以$\angle DCN = \frac{1}{2}(180^{\circ} - \angle BCD) = 55^{\circ}$。

13. 如图，AB//CD//EF，下列各式中，正确的是（ ）


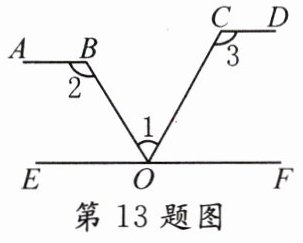
A. ∠1 + ∠2 + ∠3 = 180°
B. ∠1 + ∠2 - ∠3 = 90°
C. ∠1 - ∠2 + ∠3 = 90°
D. ∠2 + ∠3 - ∠1 = 180°

答案： D　【解析】因为$AB// CD// EF$，所以$\angle 2 + \angle BOE = 180^{\circ}$，$\angle 3 + \angle COF = 180^{\circ}$。所以$\angle BOE = 180^{\circ} - \angle 2$，$\angle COF = 180^{\circ} - \angle 3$。又因为$\angle BOE + \angle 1 + \angle COF = 180^{\circ}$，所以$(180^{\circ} - \angle 2) + \angle 1 + (180^{\circ} - \angle 3) = 180^{\circ}$。所以$\angle 2 + \angle 3 - \angle 1 = 180^{\circ}$。

14. 含30°角的直角三角板与直线l1，l2的位置关系如图所示，∠A = 30°，已知l1//l2，∠ACD = 20°，则∠1的度数为________。

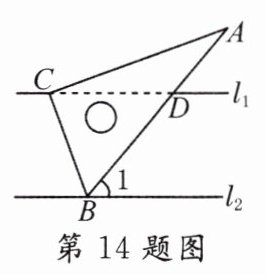
答案： $50^{\circ}$

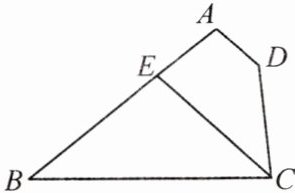
15. 如图，在四边形ABCD中，∠A = 100°，∠D = 140°，∠BCD的平分线CE交AB于点E。若CE//AD，求∠B的大小。

答案： 解:因为$CE// AD$，所以$\angle DCE + \angle D = 180^{\circ}$。所以$\angle DCE = 180^{\circ} - \angle D = 180^{\circ} - 140^{\circ} = 40^{\circ}$。因为$CE$平分$\angle BCD$，所以$\angle BCE = \angle DCE = 40^{\circ}$。因为$AD// CE$，所以$\angle BEC = \angle A = 100^{\circ}$。所以$\angle B = 180^{\circ} - 100^{\circ} - 40^{\circ} = 40^{\circ}$。

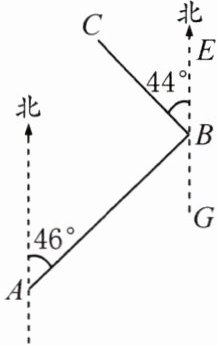
16. 如图，在A，B两地之间要修一条笔直的公路，从A地测得公路的走向是北偏东46°，A，B两地同时开工，若干天后公路准确接通。
（1）B地所修公路的走向是南偏西多少度？
（2）若公路AB长12千米，另一条公路BC长6千米，且BC的走向是北偏西44°，试求A地到公路BC的距离。

答案： 解:
(1)由两地南北方向平行，再根据内错角相等，可知$B$地所修公路的走向是南偏西$46^{\circ}$。
(2)因为$\angle ABC = 180^{\circ} - \angle ABG - \angle EBC = 180^{\circ} - 46^{\circ} - 44^{\circ} = 90^{\circ}$，所以$AB\perp BC$。所以$AB$的长度即为$A$地到公路$BC$的距离。所以$A$地到公路$BC$的距离是12千米。

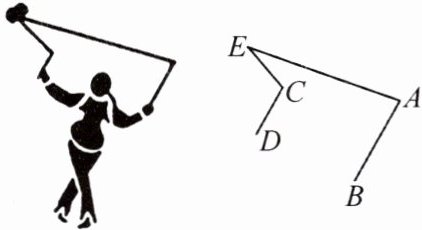
17. 为增强学生体质，弘扬中国的传统文化，学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间。如图是某同学“抖空竹”时的一个瞬间，王聪把它抽象成如图的数学问题：已知AB//CD，∠EAB = 80°，∠ECD = 110°，求∠E的度数。

答案：
解:如图所示，延长$DC$交$AE$于点$F$，
因为$AB// CD$，$\angle EAB = 80^{\circ}$，所以$\angle EAB = \angle EFC = 80^{\circ}$。因为$\angle ECD = 110^{\circ}$，所以$\angle ECF = 70^{\circ}$，所以$\angle E = 180^{\circ} - 80^{\circ} - 70^{\circ} = 30^{\circ}$。