《2025年一线调研学业测评七年级数学下册北师大版》

1. 计算：$(2a)\cdot(ab)=$ （ ）
A. $2ab$
B. $2a^{2}b$
C. $3ab$
D. $3a^{2}b$

答案： B

2. 如果$2a^{\square}b\cdot4ab = 8a^{3}b^{2}$，那么“$\square$”内应填的是 （ ）
A. 1
B. 2
C. 3
D. 4

答案： B

3. 计算$(-\frac{1}{2}x^{2}y^{3})\cdot(-4x^{2}y)$的结果是（ ）
A. $-2x^{4}y^{4}$
B. $2x^{4}y^{4}$
C. $2x^{4}y^{3}$
D. $-2x^{3}y^{3}$

答案： B

4. 如果$x^{n}y^{4}$与$2xy^{m}$相乘的结果是$2x^{5}y^{7}$，那么$mn =$______。

答案： 12

5. 一个长方体的长、宽、高分别为$4x^{2}y$，$2xy$，$\frac{1}{3}x^{3}y$，则它的体积为____________。

答案： $\frac{8}{3}x^{6}y^{3}$

6. 计算：
(1)$2xy^{2}\cdot(-3xy^{4})$；
(2)$5m^{3}n\cdot(mn)^{2}$；
(3)$(-3x^{2}y)^{2}\cdot(-2xy^{3})^{3}$。

答案：
(1) $-6x^{2}y^{6}$
(2) $5m^{5}n^{3}$
(3) $-72x^{7}y^{11}$

7. 下列运算正确的是 （ ）
A. $5x^{2}\cdot(2x^{2})^{3}=10x^{12}$
B. $(-3ab)\cdot(-2ab)^{3}=-24a^{4}b^{4}$
C. $0.1b\cdot(-10b^{2})^{3}=b^{7}$
D. $(2\times10^{n})\cdot(\frac{1}{2}\times10^{n}) = 10^{2n}$

答案： D

8. 已知$-2x^{m}y^{2}$与$4x^{2}y^{n - 1}$的积与$-x^{4}y^{3}$是同类项，则$mn =$________。

答案： 4

9. 三角$\begin{array}{c}a\\b\ \ \ \ c\end{array}$表示$3abc$，方框$\begin{array}{cc}x&w\\y&z\end{array}$表示$-4x^{y}w^{z}$，则$\begin{array}{c}m\\n\ \ \ \ 3\end{array}\times\begin{array}{cc}n&m\\2&5\end{array}=$____________。

答案：
$-36m^{6}n^{3}$ [解析] × =3×3mn×(−4n²m⁵)=−36m⁶n³。

10. 在某住房小区建设中，为了打造业主的宜居环境，该小区规划修建一个广场(平面图如图所示)，则该广场的面积为________。

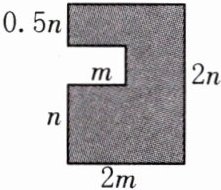
答案： $3.5mn$ [解析]广场的面积为$2m×2n−m(2n−n−0.5n)=4mn−0.5mn=3.5mn$。

11. 先化简，再求值：$2x^{2}y\cdot(-2xy^{2})^{3}+(2xy)^{3}\cdot(-xy^{2})^{2}$，其中$x = 4$，$y=\frac{1}{4}$。

答案： 解：原式$=2x^{2}y\cdot(-8x^{3}y^{6}) + 8x^{3}y^{3}\cdot x^{2}y^{4}=-16x^{5}y^{7}+8x^{5}y^{7}=-8x^{5}y^{7}$。
当$x = 4,y=\frac{1}{4}$时，
原式$=-8\times4^{5}\times(\frac{1}{4})^{7}=-\frac{1}{2}$。

12. 已知$a^{3m}=3$，$b^{3n}=2$，求$(a^{2m})^{3}+(b^{n})^{3}-a^{2m}b^{n}\cdot a^{4m}b^{2n}$的值。

答案： 解：原式$=a^{6m}+b^{3n}-a^{6m}b^{3n}=(a^{3m})^{2}+b^{3n}-(a^{3m})^{2}\cdot b^{3n}$。
因为$a^{3m}=3,b^{3n}=2$，所以原式$=3^{2}+2 - 3^{2}\times2=9 + 2 - 18=-7$。