第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1. 小明在学习中遇到这样一个问题:如图,在△ABC中,∠C>∠B,AE平分∠BAC,AD⊥BC于点D,试猜想∠B,∠C,∠EAD之间的数量关系。小明阅读题目后,没有发现数量关系与解题思路,于是尝试取几组∠B,∠C的特殊值求∠EAD的度数,得到下表中几组对应值。
|∠B的度数|20°|30°|30°|40°|
|∠C的度数|50°|60°|70°|60°|
|∠EAD的度数|15°|α|20°|β|
(1) 直接写出表中α,β的度数;
(2) 猜想∠B,∠C,∠EAD之间的数量关系,并说明理由。

|∠B的度数|20°|30°|30°|40°|
|∠C的度数|50°|60°|70°|60°|
|∠EAD的度数|15°|α|20°|β|
(1) 直接写出表中α,β的度数;
(2) 猜想∠B,∠C,∠EAD之间的数量关系,并说明理由。

答案:
1. 解:
(1)$\alpha = 15^{\circ},\beta = 10^{\circ}$。
(2)$\angle B,\angle C,\angle EAD$之间的关系是$\angle EAD=\frac{1}{2}(\angle C - \angle B)$。理由如下:
因为$AD\perp BC$,所以$\angle BAD = 90^{\circ}-\angle B$。因为$\angle BAC = 180^{\circ}-(\angle B+\angle C)$,$AE$平分$\angle BAC$,所以$\angle BAE=\frac{1}{2}\angle BAC = 90^{\circ}-\frac{1}{2}(\angle B+\angle C)$。因为$\angle EAD=\angle BAD - \angle BAE$,所以$\angle EAD = 90^{\circ}-\angle B - 90^{\circ}+\frac{1}{2}(\angle B+\angle C)=\frac{1}{2}(\angle C - \angle B)$。
(1)$\alpha = 15^{\circ},\beta = 10^{\circ}$。
(2)$\angle B,\angle C,\angle EAD$之间的关系是$\angle EAD=\frac{1}{2}(\angle C - \angle B)$。理由如下:
因为$AD\perp BC$,所以$\angle BAD = 90^{\circ}-\angle B$。因为$\angle BAC = 180^{\circ}-(\angle B+\angle C)$,$AE$平分$\angle BAC$,所以$\angle BAE=\frac{1}{2}\angle BAC = 90^{\circ}-\frac{1}{2}(\angle B+\angle C)$。因为$\angle EAD=\angle BAD - \angle BAE$,所以$\angle EAD = 90^{\circ}-\angle B - 90^{\circ}+\frac{1}{2}(\angle B+\angle C)=\frac{1}{2}(\angle C - \angle B)$。
2. 已知:在四边形ABCD中,AB = AD,∠B + ∠D = 180°,E,F分别是边BC,CD上的点,且∠EAF = $\frac{1}{2}$∠BAD。
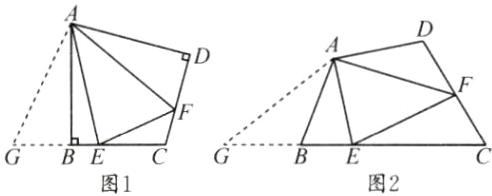
(1) 为探究上述问题,小宁同学先画出了其中一种特殊情况,如图1,当∠B = ∠D = 90°时,小宁同学探究此问题的方法是:延长EB到点G,使BG = DF,连接AG,请你在图1中添加上述辅助线,并补全下面的思路。
小宁的解题思路是:先说明△ABG≌________;再说明△AEG≌________;即可得出BE,EF,FD之间的数量关系是________________。
(2) 请你借鉴小宁的方法探究图2,当∠B + ∠D = 180°时,(1)中的结论是否仍然成立?请说明理由。
(1) 为探究上述问题,小宁同学先画出了其中一种特殊情况,如图1,当∠B = ∠D = 90°时,小宁同学探究此问题的方法是:延长EB到点G,使BG = DF,连接AG,请你在图1中添加上述辅助线,并补全下面的思路。
小宁的解题思路是:先说明△ABG≌________;再说明△AEG≌________;即可得出BE,EF,FD之间的数量关系是________________。
(2) 请你借鉴小宁的方法探究图2,当∠B + ∠D = 180°时,(1)中的结论是否仍然成立?请说明理由。
答案:
解:
(1)$\triangle ADF$ $\triangle AEF$ $EF = BE + FD$
补全图形如图1所示。
(2)
(1)中的结论$EF = BE + FD$仍然成立。理由:
如图2,延长$EB$到$G$,使$BG = DF$,连接$AG$。
因为$\angle ABC+\angle D = 180^{\circ},\angle ABG+\angle ABC = 180^{\circ}$,所以$\angle D=\angle ABG$。
在$\triangle GAB$与$\triangle FAD$中,因为$AB = AD,\angle ABG=\angle D,BG = DF$,
所以$\triangle GAB\cong\triangle FAD(SAS)$,所以$AG = AF,\angle BAG=\angle DAF$。
因为$\angle EAF=\frac{1}{2}\angle BAD$,所以$\angle GAE=\angle BAG+\angle BAE=\angle DAF+\angle BAE=\angle BAD - \angle EAF=\frac{1}{2}\angle BAD=\angle EAF$。
又因为$AE = AE$,
所以$\triangle AEG\cong\triangle AEF(SAS)$,
所以$EF = EG$。
因为$EG = BE + BG$,所以$EF = BE + FD$。
解:
(1)$\triangle ADF$ $\triangle AEF$ $EF = BE + FD$
补全图形如图1所示。

(2)
(1)中的结论$EF = BE + FD$仍然成立。理由:
如图2,延长$EB$到$G$,使$BG = DF$,连接$AG$。
因为$\angle ABC+\angle D = 180^{\circ},\angle ABG+\angle ABC = 180^{\circ}$,所以$\angle D=\angle ABG$。
在$\triangle GAB$与$\triangle FAD$中,因为$AB = AD,\angle ABG=\angle D,BG = DF$,
所以$\triangle GAB\cong\triangle FAD(SAS)$,所以$AG = AF,\angle BAG=\angle DAF$。
因为$\angle EAF=\frac{1}{2}\angle BAD$,所以$\angle GAE=\angle BAG+\angle BAE=\angle DAF+\angle BAE=\angle BAD - \angle EAF=\frac{1}{2}\angle BAD=\angle EAF$。
又因为$AE = AE$,
所以$\triangle AEG\cong\triangle AEF(SAS)$,
所以$EF = EG$。
因为$EG = BE + BG$,所以$EF = BE + FD$。
查看更多完整答案,请扫码查看


