第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
9. (济宁中考)如图,AB//CD,BC//DE,若∠B = 72°28',那么∠D的度数是( )

A. 72°28'
B. 101°28'
C. 107°32'
D. 127°32'

A. 72°28'
B. 101°28'
C. 107°32'
D. 127°32'
答案:
C
10. 生活中常见的探照灯、汽车大灯等灯具都与抛物线有关。如图,从光源P点照射到抛物线上的光线PA,PB
等反射以后沿着与直线PF平行的方向射出,若∠CAP = α,∠DBP = β,则∠APB的度数为( )
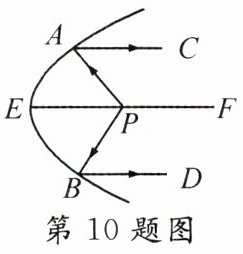
A. 2α
B. 2β
C. α + β
D. $\frac{5}{4}$(α + β)
等反射以后沿着与直线PF平行的方向射出,若∠CAP = α,∠DBP = β,则∠APB的度数为( )

A. 2α
B. 2β
C. α + β
D. $\frac{5}{4}$(α + β)
答案:
C
11. 如图,若∠1 = ∠2,DE//BC,则有下列结论:
①FG//DC;②∠AED = ∠ACB;③CD平分∠ACB;④∠1 + ∠B = 90°;⑤∠BFG = ∠BDC。其中正确的结论是( )
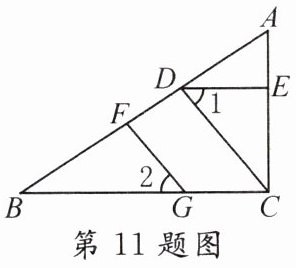
A. ①②③
B. ①②⑤
C. ①③④
D. ③④
①FG//DC;②∠AED = ∠ACB;③CD平分∠ACB;④∠1 + ∠B = 90°;⑤∠BFG = ∠BDC。其中正确的结论是( )

A. ①②③
B. ①②⑤
C. ①③④
D. ③④
答案:
B 【解析】因为$DE// BC$,所以$\angle 1 = \angle BCD$,又因为$\angle 1 = \angle 2$,所以$\angle BCD = \angle 2$,所以$FG// DC$,故①正确;因为$DE// BC$,所以$\angle AED = \angle ACB$,故②正确;因为$FG// DC$,所以$\angle BFG = \angle BDC$,故⑤正确。由已知条件无法确定③④正确。
12. 如图,一辆汽车经过两次转弯后,行驶的方向与原来保持平行,如果第一次转过的角α为64°,则第二次转过的角β为______°。
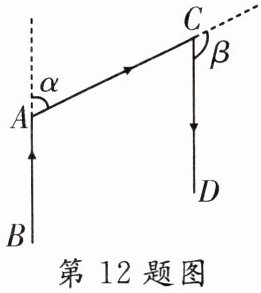

答案:
116
13. 如图,直线BD分别交射线AE,CF于点B,D,连接AD和BC,∠1 + ∠2 = 180°,∠A = ∠C,AD平分∠BDF,试说明:
(1)AD//BC。
(2)BC平分∠DBE。
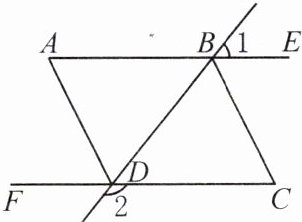
(1)AD//BC。
(2)BC平分∠DBE。

答案:
解:
(1)因为$\angle 2 + \angle BDC = 180^{\circ}$,$\angle 1 + \angle 2 = 180^{\circ}$,所以$\angle 1 = \angle BDC$。所以$AB// CF$。所以$\angle C = \angle EBC$。又因为$\angle A = \angle C$,所以$\angle A = \angle EBC$。所以$AD// BC$。
(2)因为$AD$平分$\angle BDF$,所以$\angle FDA = \angle ADB$。因为$AD// BC$,所以$\angle FDA = \angle C$,$\angle ADB = \angle DBC$。又因为$\angle C = \angle EBC$,所以$\angle EBC = \angle DBC$。所以$BC$平分$\angle DBE$。
(1)因为$\angle 2 + \angle BDC = 180^{\circ}$,$\angle 1 + \angle 2 = 180^{\circ}$,所以$\angle 1 = \angle BDC$。所以$AB// CF$。所以$\angle C = \angle EBC$。又因为$\angle A = \angle C$,所以$\angle A = \angle EBC$。所以$AD// BC$。
(2)因为$AD$平分$\angle BDF$,所以$\angle FDA = \angle ADB$。因为$AD// BC$,所以$\angle FDA = \angle C$,$\angle ADB = \angle DBC$。又因为$\angle C = \angle EBC$,所以$\angle EBC = \angle DBC$。所以$BC$平分$\angle DBE$。
14. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知小敏画平行线的依据可以是________。(把所有正确结论的序号都填在横线上)
①如果两条直线和第三条直线平行,那么这两条直线平行;②同位角相等,两直线平行;③两直线平行,内错角相等;④同旁内角互补,两直线平行。

①如果两条直线和第三条直线平行,那么这两条直线平行;②同位角相等,两直线平行;③两直线平行,内错角相等;④同旁内角互补,两直线平行。

答案:
②④
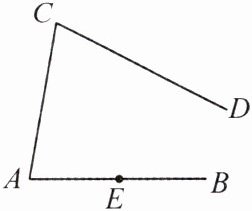
15. 如图,已知∠C = 75°,点E在AB上。
(1)以E为顶点,作EF//AC,与CD交于点F。(保留作图痕迹,不必写作法)
(2)在(1)的条件下,求∠CFE的度数。
(1)以E为顶点,作EF//AC,与CD交于点F。(保留作图痕迹,不必写作法)
(2)在(1)的条件下,求∠CFE的度数。

答案:
解:
(1)作图如图所示。
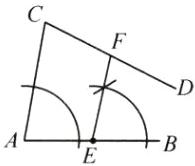
(2)因为$EF// AC$,所以$\angle C + \angle CFE = 180^{\circ}$。因为$\angle C = 75^{\circ}$,所以$\angle CFE = 180^{\circ} - 75^{\circ} = 105^{\circ}$。
解:
(1)作图如图所示。

(2)因为$EF// AC$,所以$\angle C + \angle CFE = 180^{\circ}$。因为$\angle C = 75^{\circ}$,所以$\angle CFE = 180^{\circ} - 75^{\circ} = 105^{\circ}$。
查看更多完整答案,请扫码查看


