《2025年一线调研学业测评七年级数学下册北师大版》

11. 已知：$OC$平分$\angle AOB$，点$P$，$Q$是$OC$上不同的点，$PE\perp OA$，$PF\perp OB$，垂足分别为$E$，$F$，连接$EQ$，$FQ$。试说明：
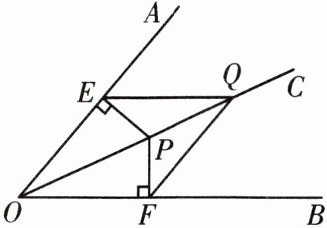
(1)$\triangle OPE\cong\triangle OPF$。
(2)$FQ = EQ$。

答案： 解：
(1) 因为 $OC$ 平分 $\angle AOB$，所以 $\angle AOC = \angle BOC$。因为 $PE\perp OA$，$PF\perp OB$，所以 $\angle PEO = \angle PFO = 90^{\circ}$。又因为 $OP = OP$，所以 $\triangle OPE\cong\triangle OPF(AAS)$。
(2) 因为 $\triangle OPE\cong\triangle OPF$，所以 $OE = OF$。又因为 $\angle EOQ = \angle FOQ$，$OQ = OQ$，所以 $\triangle OEQ\cong\triangle OFQ(SAS)$，所以 $EQ = FQ$。

12. (1)如图①，在$\triangle AOB$和$\triangle COD$中，$OA = OB$，$OC = OD$，$\angle AOB=\angle COD = 50^{\circ}$。试说明：$AC = BD$，$\angle APB = 50^{\circ}$。
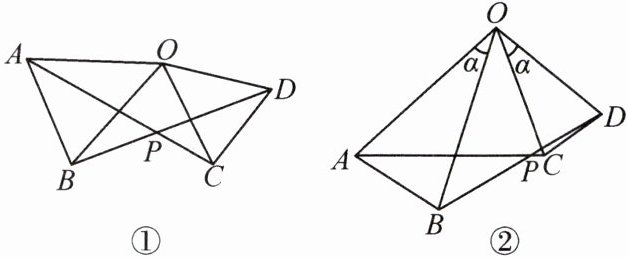
(2)如图②，在$\triangle AOB$和$\triangle COD$中，$OA = OB$，$OC = OD$，$\angle AOB=\angle COD=\alpha$，求$AC$与$BD$间的数量关系和$\angle APB$的大小。

答案： 解：
(1) 因为 $\angle AOB = \angle COD = 50^{\circ}$，所以 $\angle AOB + \angle BOC = \angle DOC + \angle BOC$，即 $\angle AOC = \angle BOD$。在 $\triangle AOC$ 和 $\triangle BOD$ 中，因为 $OA = OB$，$\angle AOC = \angle BOD$，$OC = OD$，所以 $\triangle AOC\cong\triangle BOD$。所以 $AC = BD$，$\angle CAO = \angle DBO$。根据三角形内角和可知 $\angle CAO + \angle AOB = \angle DBO + \angle APB$，所以 $\angle APB = \angle AOB = 50^{\circ}$。
(2) 因为 $\angle AOB = \angle COD = \alpha$，所以 $\angle AOC = \angle BOD$。在 $\triangle AOC$ 和 $\triangle BOD$ 中，因为 $OA = OB$，$\angle AOC = \angle BOD$，$OC = OD$，所以 $\triangle AOC\cong\triangle BOD$。所以 $AC = BD$，$\angle CAO = \angle DBO$。根据三角形内角和可知 $\angle CAO + \angle AOB = \angle DBO + \angle APB$，所以 $\angle APB = \angle AOB = \alpha$。

13. 农科所有一块五边形的试验田如图所示，已知在五边形$ABCDE$中，$\angle ABC=\angle AED = 90^{\circ}$，$AB = CD = AE = BC + DE = 20\text{m}$，则这块试验田的面积为_________。

答案：
$400m^{2}$ 【解析】如图，在 $CB$ 的延长线上截取 $BD' = ED$，连接 $AD'$，$AC$，$AD$。 易说明 $\triangle ADE\cong\triangle AD'B$。所以 $AD = AD'$，$DE = D'B$。又因为 $BC + DE = CD$，所以 $BC + D'B = CD' = CD$。又因为 $AC = AC$，$AD' = AD$，所以 $\triangle ACD'\cong\triangle ACD$。所以 $S_{试验田}=S_{四边形ADCD'}=2S_{\triangle ACD'}=2\times\frac{1}{2}CD'\times AB = 2\times\frac{1}{2}\times20\times20 = 400(m^{2})$。

14. 杨阳同学沿一段笔直的人行道行走，在由$A$处步行到$B$处的过程中，通过隔离带的空隙$O$，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息汇集如下：
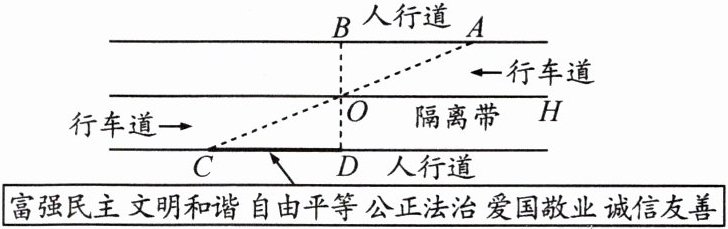
如图，$AB// OH// CD$，相邻两平行线间的距离相等，$AC$，$BD$相交于点$O$，$OD\perp CD$，垂足为$D$。已知$AB = 20$米，请根据上述信息求标语$CD$的长度。

答案： 解：因为 $AB// CD$，所以 $\angle ABO = \angle CDO$。因为 $OD\perp CD$，所以 $\angle CDO = 90^{\circ}$。所以 $\angle ABO = 90^{\circ}$。又因为相邻两平行线间的距离相等，所以 $OD = OB$。在 $\triangle ABO$ 和 $\triangle CDO$ 中，因为 $\angle ABO = \angle CDO$，$OB = OD$，$\angle AOB = \angle COD$，所以 $\triangle ABO\cong\triangle CDO$。所以 $CD = AB = 20$ 米。所以标语 $CD$ 的长度为 20 米。