《2025年一线调研学业测评七年级数学下册北师大版》

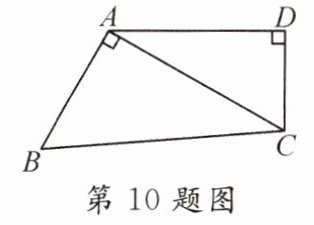
10. 如图，已知A，B，C，D是某公园内的四个凉亭，图中的连线是甬道，且∠D = 90°，∠BAC = 90°，若AC = 100m，则下列判断中不正确的是（ ）


A. 甬道AD可能为100m
B. 甬道CD可能为60m
C. 甬道AD可能为80m
D. 甬道BC可能为140m

答案： A

11. 易错题已知OA⊥OB，O为垂足，且∠AOC∶∠AOB = 1∶2，则∠BOC的度数是（ ）
A. 45°
B. 135°
C. 45°或135°
D. 60°或20°

答案： C [解析]分两种情况:当OC在∠AOB的内侧时，∠BOC = $\frac{1}{2}\times90^{\circ}=45^{\circ}$；当OC在∠AOB的外侧时，∠BOC = $\frac{3}{2}\times90^{\circ}=135^{\circ}$。

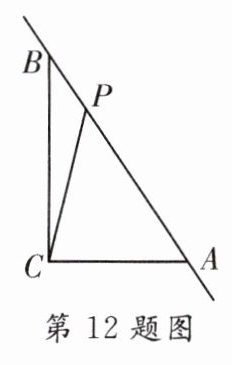
12. 如图，在△ABC中，∠ACB = 90°，AC = 6，BC = 8，AB = 10，P为直线AB上一动点，连接PC，则线段PC的最小值是（ ）


A. 4
B. 4.5
C. 4.8
D. 5

答案： C

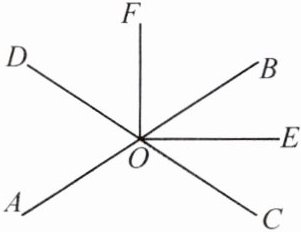
13. 如图所示，直线AB，CD相交于点O，OE平分∠BOC，OF⊥OE，且∠AOC = 114°，求∠BOF的度数。

答案： 解:因为∠AOC = 114°，所以∠BOC = 66°。因为OE平分∠BOC，所以∠BOE = ∠COE = $\frac{1}{2}$∠BOC = 33°。因为OF⊥OE，所以∠FOE = 90°。所以∠BOF = ∠FOE - ∠BOE = 90° - 33° = 57°。

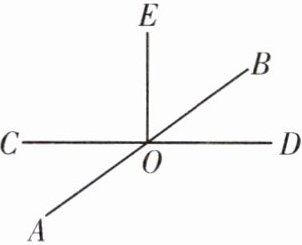
14. 如图，已知直线AB，CD相交于点O，EO⊥CD于点O。
（1）若∠AOC = 36°，求∠BOE的度数。
（2）若∠BOD∶∠BOC = 1∶5，求∠AOE的度数。
（3）在（2）的条件下，请你过点O画直线MN⊥AB，并在直线MN上取一点F（点F与点O不重合），然后求出∠EOF的度数。

答案：
解:
(1)因为EO⊥CD，所以∠DOE = 90°。又因为∠BOD = ∠AOC = 36°，所以∠BOE = ∠DOE - ∠BOD = 90° - 36° = 54°。
(2)因为∠BOD + ∠BOC = 180°，∠BOD：∠BOC = 1：5，所以∠BOD = 180°×$\frac{1}{5 + 1}$= 30°。所以∠AOC = 30°。又因为EO⊥CD，所以∠COE = 90°。所以∠AOE = 90° + 30° = 120°。
(3)分两种情况:如图，若点F在射线OM上，因为EO⊥CD，MN⊥AB，所以∠COE = ∠AOM = 90°，所以∠COE - ∠COM = ∠AOM - ∠COM，即∠EOF = ∠AOC = 30°。若F在射线ON上，即为图中F'的位置，则∠EOF' = ∠DOE + ∠BON - ∠BOD = 90° + 90° - 30° = 150°。综上所述，∠EOF的度数为30°或150°。