《2025年5年中考3年模拟九年级数学下册湘教版》

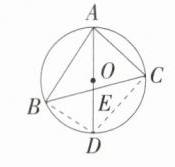
8.(2024陕西西安雁塔曲江一中二模)如图，$\odot O$是$\triangle ABC$的外接圆，$AD$为$\odot O$的直径，交$BC$于点$E$，若点$C$为弧$ACD$的中点，弦$AB=\sqrt{3}DO$，则$\angle BED$的度数为 ( )

A.$60^{\circ}$
B.$65^{\circ}$
C.$70^{\circ}$
D.$75^{\circ}$

答案：
D：如图，连接$BD$，$CD$，$\because AD$为$\odot O$的直径，$\therefore \angle ABD=\angle ACD = 90^{\circ}$。$\because AB=\sqrt{3}DO$，$AD = 2OD$，$\therefore \sin\angle ADB=\frac{AB}{AD}=\frac{\sqrt{3}}{2}$，$\therefore \angle ADB = 60^{\circ}$，$\therefore \angle ACB=\angle ADB = 60^{\circ}$。$\because$点$C$为弧$ACD$的中点，$\therefore \angle DAC=\angle ADC = 45^{\circ}$，$\therefore \angle BED=\angle AEC = 180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$，故选 D。

9.(2024山西忻州保德三模)“科教兴国，强国有我”.某中学在科技实验活动中，设计并进行了“水火箭”升空实验，已知“水火箭”的升空高度$h$(m)与飞行时间$t$(s)满足函数关系式$h = at^{2}+bt + 1$.“水火箭”飞行3 s和飞行9 s时的升空高度相同，飞行8 s时的升空高度为33 m，则“水火箭”升空的最大高度为 ( )
A.33 m
B.36 m
C.37 m
D.40 m

答案： C：$\because$“水火箭”飞行$3$s 和飞行$9$s 时的升空高度相同，$\therefore -\frac{b}{2a}=\frac{3 + 9}{2}=6$，$\therefore b=-12a$，$\therefore h = at^{2}-12at + 1$。把$t = 8$，$h = 33$代入，得$64a-96a + 1 = 33$，解得$a=-1$，$\therefore h=-t^{2}+12t + 1=-(t - 6)^{2}+37$。$\because -1\lt0$，$\therefore$当$t = 6$时，$h$取得最大值，为 37，即“水火箭”升空的最大高度为 37m，故选 C。

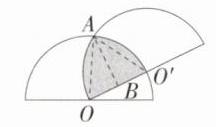
10.(2024山东泰安中考)两个半径相等的半圆按如图所示的方式放置，半圆$O'$的一个直径端点与半圆$O$的圆心重合，若半圆的半径为2，则图中阴影部分的面积是 ( )

A.$\frac{4}{3}\pi-\sqrt{3}$
B.$\frac{4}{3}\pi$
C.$\frac{2}{3}\pi-\sqrt{3}$
D.$\frac{4}{3}\pi-\frac{\sqrt{3}}{4}$

答案：
A：如图，设两半圆的交点为$A$，连接$OA$，$AO'$，过点$A$作$AB\perp OO'$于点$B$，$\because OA = OO' = AO' = 2$，$\therefore \triangle AOO'$是等边三角形，$\therefore \angle AOO' = 60^{\circ}$，$OB=\frac{1}{2}OO' = 1$，$\therefore AB=\sqrt{2^{2}-1^{2}}=\sqrt{3}$，$\therefore S_{弓形AO'}=S_{扇形AOO'}-S_{\triangle AOO'}=\frac{60\pi\times2^{2}}{360}-\frac{1}{2}\times2\times\sqrt{3}=\frac{2}{3}\pi-\sqrt{3}$，$\therefore S_{阴影}=S_{弓形AO'}+S_{扇形AO'O}=\frac{2}{3}\pi-\sqrt{3}+\frac{2}{3}\pi=\frac{4}{3}\pi-\sqrt{3}$。故选 A。

11.(新独家原创)“目前，西湖是我国第一大淡水湖”是________事件.(填“随机”“必然”或“不可能”)

答案： 不可能
解析：目前，鄱阳湖是我国第一大淡水湖，所以“目前，西湖是我国第一大淡水湖”是不可能事件。

12.(2023湖南永州中考)甲、乙两队学生参加学校拉拉队选拔，两队队员的平均身高均为1.72 m，甲队队员的身高的方差为1.2，乙队队员的身高的方差为5.6.若要求拉拉队队员的身高比较整齐，则应选择________队.

答案： 甲
解析：$\because \overline{x}_{甲}=\overline{x}_{乙}$，$s_{甲}^{2}=1.2$，$s_{乙}^{2}=5.6$，$\therefore s_{甲}^{2}\lt s_{乙}^{2}$，$\therefore$应选择甲队。

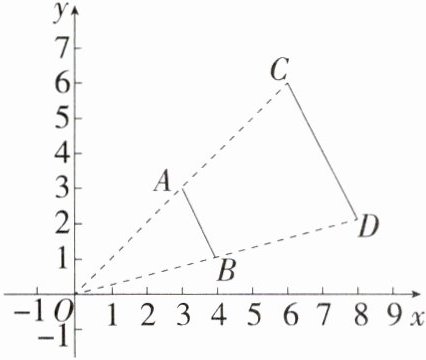
13.(2024湖南衡阳蒸湘一模)如图，线段$AB$两个端点的坐标分别为$A(3,3)$、$B(4,1)$，以原点$O$为位似中心，在第一象限内将线段$AB$放大为原来的2倍后得到线段$CD$，则端点$C$的坐标为________.

答案： $(6,6)$
解析：$\because$以原点$O$为位似中心，在第一象限内将线段$AB$放大为原来的 2 倍后得到线段$CD$，$A$点的对应点是$C$点，$A(3,3)$，$\therefore C(6,6)$。

14.(2024四川甘孜州中考)某校组织多项活动加强科学教育，八年级(一)班分两批次确定项目组成员，参加“实践探究”活动，第一批次确定了7人，第二批次确定了1名男生、2名女生.现从项目组中随机抽取1人承担联络任务，若抽中男生的概率为$\frac{3}{5}$，则第一批次确定的人员中，男生有________人.

答案： 5
解析：设第一批次确定的人员中，男生有$x$人，则$\frac{x + 1}{7+1+2}=\frac{3}{5}$，解得$x = 5$，即第一批次确定的人员中，男生有 5 人。

15.(2023湖南娄底中考)如图，在$\triangle ABC$中，$AC = 3$，$AB = 4$，$BC$边上的高$AD = 2$，将$\triangle ABC$绕着$BC$所在的直线旋转一周得到的几何体的表面积为________.

答案： $14\pi$
解析：所得几何体为两个同底圆锥的组合体，几何体的表面积是两个圆锥的侧面积之和。这两个圆锥的底面圆半径均为 2，母线长分别为 3 和 4，故得到的几何体的表面积为$\pi\times2\times3+\pi\times2\times4 = 14\pi$。