《2025年5年中考3年模拟九年级数学下册湘教版》

1.(2024湖南中考)如图,AB,AC为⊙O的两条弦,连接OB,OC,若∠A = 45°,则∠BOC的度数为 ( )

A.60°
B.75°
C.90°
D.135°

答案： C $\because\overset{\frown}{BC}=\overset{\frown}{BC}$，$\therefore\angle A = \frac{1}{2}\angle BOC$。又$\because\angle A = 45^{\circ}$，$\therefore\angle BOC = 2\times45^{\circ}=90^{\circ}$。故选 C。

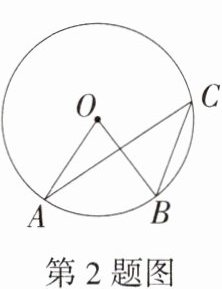
2.新独家原创 如图,点A、B、C在⊙O上,圆心角∠O的度数为(m + 36)°,圆周角∠C的度数为(m - 2)°,则m的值为 ( )

A.36
B.38
C.40
D.42

答案： C $\because\overset{\frown}{AB}=\overset{\frown}{AB}$，$\therefore\angle O = 2\angle C$，$\therefore m + 36 = 2(m - 2)$，解得$m = 40$，故选 C。

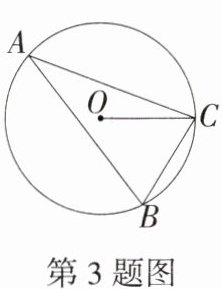
3.(2024湖南娄底新化期末)如图,已知⊙O的半径OC = 3,∠BAC = 30°,则弦BC的长度为 ( )

A.3
B.$\frac{3}{2}$
C.3$\sqrt{2}$
D.2$\sqrt{3}$

答案： A 连接$OB$，由圆周角定理得$\angle BOC = 2\angle BAC = 60^{\circ}$。又$\because OB = OC$，$\therefore\triangle BOC$为等边三角形，$\therefore BC = OC = 3$。故选 A。

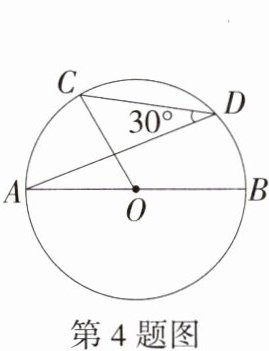
4.(2022湖南永州中考)如图,AB是⊙O的直径,点C、D在⊙O上,∠ADC = 30°,则∠BOC = ______度.(M9202002)

答案：   120
解析 由圆周角定理得$\angle AOC = 2\angle ADC = 2\times30^{\circ}=60^{\circ}$，$\therefore\angle BOC = 180^{\circ}-\angle AOC = 180^{\circ}-60^{\circ}=120^{\circ}$。

5.如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD = ( )

A.∠ACD
B.∠ADB
C.∠AED
D.∠ACB

答案： A $\because\angle ABD$所对的弧是$\overset{\frown}{AD}$，$\angle ACD$所对的弧也是$\overset{\frown}{AD}$，$\therefore\angle ABD = \angle ACD$。故选 A。

6.一题多解 (2024云南中考)如图,CD是⊙O的直径,点A,B在⊙O上.若$\overset{\frown}{AC}$=$\overset{\frown}{BC}$,∠AOC = 36°,则∠D = (M9202002) ( )

A.9°
B.18°
C.36°
D.45°

答案： B 【解法一】等弧圆周角法：连接$AD$，$\because\overset{\frown}{AC}=\overset{\frown}{BC}$，$\therefore\angle BDC = \angle ADC = \frac{1}{2}\angle AOC = \frac{1}{2}\times36^{\circ}=18^{\circ}$，故选 B。
【解法二】等弧圆心角法：连接$OB$，$\because\overset{\frown}{AC}=\overset{\frown}{BC}$，$\therefore\angle BOC = \angle AOC = 36^{\circ}$，$\therefore\angle D = \frac{1}{2}\angle BOC = \frac{1}{2}\times36^{\circ}=18^{\circ}$，故选 B。

7.情境题·现实生活 (2023湖南郴州中考,15,★☆☆)如图,某博览会上有一圆形展示区,在其圆形边缘的点P处安装了一台监视器,它的监控角度是55°,为了监控整个展区,最少需要在圆形边缘上共安装这样的监视器________台.(M9202003)

答案：   4
解析 $\because\angle P = 55^{\circ}$，$\therefore\angle P$所对弧所对的圆心角是$110^{\circ}$。$\because360^{\circ}\div110^{\circ}=3\frac{3}{11}$，$\therefore$最少需要在圆形边缘上共安装这样的监视器 4 台。

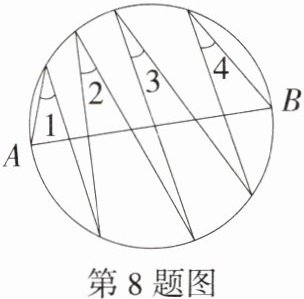
8.(2024江苏连云港中考,14,★☆☆)如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1 + ∠2 + ∠3 + ∠4 = ________°.(M9202002)

答案：   90
解析 $\because AB$是圆的直径，$\therefore AB$所对的弧是半圆，所对圆心角的度数为$180^{\circ}$，$\because\angle1$、$\angle2$、$\angle3$、$\angle4$所对的弧的和为半圆，$\therefore\angle1+\angle2+\angle3+\angle4 = \frac{1}{2}\times180^{\circ}=90^{\circ}$。

9.(2022湖南怀化中考,20,★☆☆)如图,点A,B,C,D在⊙O上,$\overset{\frown}{AB}$=$\overset{\frown}{CD}$.求证：
(1)AC = BD;
(2)△ABE∽△DCE.

答案： 证明
(1)$\because\overset{\frown}{AB}=\overset{\frown}{CD}$，$\therefore\overset{\frown}{AC}=\overset{\frown}{BD}$，$\therefore AC = BD$。
(2)$\because\angle A = \angle D$，$\angle B = \angle C$，$\therefore\triangle ABE\backsim\triangle DCE$。