《2025年5年中考3年模拟九年级数学下册湘教版》

1.(2024安徽滁州期末)二次函数$y=(a - 1)x^{2}$的图象是一条抛物线，若该抛物线开口向上，则a的取值范围是(M9201002) ( )
A.$a\geqslant1$
B.$a＞1$
C.$a\leqslant1$
D.$a＜1$

答案： B：
∵ 抛物线 $y=(a - 1)x^{2}$ 的开口向上，
∴ $a - 1＞0$，解得 $a＞1$，故选 B。

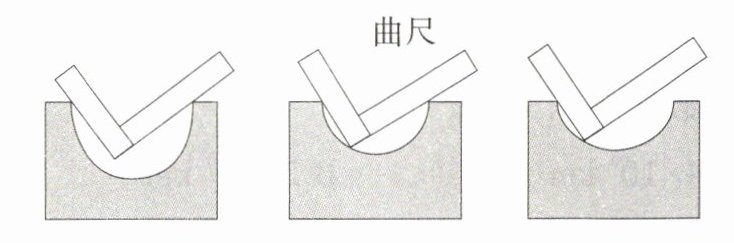
2.(2024湖南长沙雨雅礼实验中学月考)如图，用直角曲尺检查半圆形的工件是否合格，原理是(M9202002) ( )


A.同弧所对的圆周角相等
B.直径是圆中最大的弦
C.$90^{\circ}$圆周角所对的弦是直径
D.圆上各点到圆心的距离相等

答案： C：直角曲尺放入半圆形工件的部分是直角，若直角顶点能碰到半圆，则说明此工件是半圆，原理是 $90^{\circ}$ 圆周角所对的弦是直径。故选 C。

3. 跨艺术·青铜雕塑(2024湖南长沙一模)如图，《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕塑，掷铁饼者张开的双臂与肩宽可以近似看作一张拉满弦的弓.若“弓”所对的圆心角$\alpha$的度数为$100^{\circ}$，“弓”所在圆的半径为1.2米，则“弓”的长度为(M9202006) ( )


A.$\frac{2}{3}\pi$米
B.$\frac{3}{2}\pi$米
C.$\frac{1}{2}\pi$米
D.$\frac{2}{5}\pi$米

答案： A：“弓”的长度为 $\frac{100\pi\times1.2}{180}=\frac{2}{3}\pi$（米）。故选 A。

4.(2023江苏宿迁中考)在同一平面内，已知$\odot O$的半径为2，圆心O到直线l的距离为3，点P为圆上的一个动点，则点P到直线l的最大距离是(M9202001) ( )
A.2
B.5
C.6
D.8

答案：
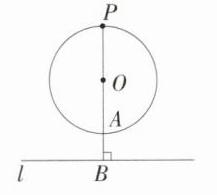
B：如图，由题意得 $OA = 2$，$OB = 3$，当点 $P$ 是 $BO$ 的延长线与 $\odot O$ 的交点时，点 $P$ 到直线 $l$ 的距离最大，此时点 $P$ 到直线 $l$ 的距离是 $3 + 2 = 5$，故选 B。

5.(2024重庆育才中学教育集团期末)某农机厂四月份生产零件60万个，设该厂第二季度平均每月的增长率为x，如果第二季度共生产零件y万个，那么y与x满足的函数关系式是 ( )
A.$y = 60(1 + x)^{2}$
B.$y = 60 + 60(1 + x) + 60(1 + x)^{2}$
C.$y = 60(1 + x) + 60(1 + x)^{2}$
D.$y = 60 + 60(1 + x)$

答案： B：该厂第二季度平均每月的增长率为 $x$，则五月份生产零件 $60(1 + x)$ 万个，六月份生产零件 $60(1 + x)^{2}$ 万个，根据第二季度共生产零件 $y$ 万个，得 $y = 60+60(1 + x)+60(1 + x)^{2}$。故选 B。

6.(2024湖南长沙岳麓麓实验中学三模)如图，四边形ABCD内接于$\odot O$，$AB = CD$，连接$OA$，$OC$.若$\angle BAD = 80^{\circ}$，则$\angle AOC$的度数为 ( )


A.$100^{\circ}$
B.$160^{\circ}$
C.$120^{\circ}$
D.$135^{\circ}$

答案： B：
∵ $AB = CD$，
∴ $\overset{\frown}{AB}=\overset{\frown}{CD}$，
∴ $\overset{\frown}{AC}=\overset{\frown}{BD}$，
∴ $\angle D=\angle BAD = 80^{\circ}$，
∴ $\angle AOC = 2\angle D = 160^{\circ}$，故选 B。

7.(2024贵州中考)如图，二次函数$y = ax^{2} + bx + c$的部分图象与x轴的一个交点的横坐标是-3，顶点坐标为(-1,4)，则下列说法正确的是 ( )


A.二次函数图象的对称轴是直线$x = 1$
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当$x＜-1$时，$y$随$x$的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3

答案： D：
∵ 顶点坐标为 $(-1,4)$，
∴ 二次函数图象的对称轴为直线 $x = -1$，故选项 A 错误。
∵ 点 $(-3,0)$ 关于直线 $x = -1$ 的对称点为点 $(1,0)$，
∴ 二次函数图象与 $x$ 轴的另一个交点的横坐标是 $1$，故选项 B 错误。由图象可知当 $x＜-1$ 时，$y$ 随 $x$ 的增大而增大，故选项 C 错误。设二次函数解析式为 $y = a(x + 1)^{2}+4$，将 $(-3,0)$ 代入，解得 $a = -1$，
∴ $y = -(x + 1)^{2}+4$，令 $x = 0$，得 $y = 3$，
∴ 二次函数图象与 $y$ 轴的交点的纵坐标是 $3$，故选项 D 正确。故选 D。

8.(2023湖南长沙一中教育集团期中)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边长作一个三角形，则该三角形是(M9202007) ( )
A.钝角三角形
B.锐角三角形
C.等腰三角形
D.直角三角形

答案：
D：如图 1，易知 $\angle OCD = 30^{\circ}$，
∵ $OC = 2$，
∴ $OD=\frac{1}{2}OC = 1$；如图 2，易知 $\triangle OBE$ 为等腰直角三角形，
∵ $OB = 2$，
∴ $OE=\sqrt{2}$；如图 3，易知 $\angle AOD = 30^{\circ}$，
∵ $OA = 2$，
∴ $AD=\frac{1}{2}OA = 1$，
∴ $OD=\sqrt{OA^{2}-AD^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$，
∵ $1^{2}+(\sqrt{2})^{2}=(\sqrt{3})^{2}$，
∴ 该三角形是直角三角形。故选 D。