第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024北京期中)如图,AB为⊙O的直径,点C是⊙O上的一点,∠ABC = 70°,则∠BAC = ( )
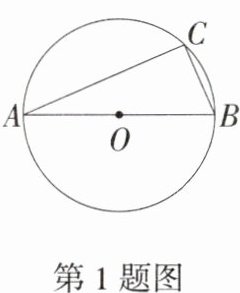
A.50°
B.40°
C.30°
D.20°

A.50°
B.40°
C.30°
D.20°
答案:
D
∵AB为⊙O的直径,
∴∠ACB = 90°.
∵∠ABC = 70°,
∴∠BAC = 90° - ∠ABC = 90° - 70° = 20°.故选D.
∵AB为⊙O的直径,
∴∠ACB = 90°.
∵∠ABC = 70°,
∴∠BAC = 90° - ∠ABC = 90° - 70° = 20°.故选D.
2.(2024湖南邵阳模拟)如图,AB为⊙O的直径,∠ABC = 36°,则∠CDB = (M9202002) ( )
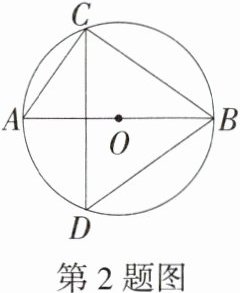
A.36°
B.72°
C.64°
D.54°

A.36°
B.72°
C.64°
D.54°
答案:
D
∵AB为⊙O的直径,
∴∠ACB = 90°,
∴∠CAB + ∠ABC = 90°,
∵∠ABC = 36°,
∴∠CAB = 54°,
∴∠CDB = ∠CAB = 54°,故选D.
∵AB为⊙O的直径,
∴∠ACB = 90°,
∴∠CAB + ∠ABC = 90°,
∵∠ABC = 36°,
∴∠CAB = 54°,
∴∠CDB = ∠CAB = 54°,故选D.
3.(2024湖南衡阳模拟)如图,AB是⊙O的直径,弦CD//AB,若∠ACD = 26°,则∠ABC = ______°.
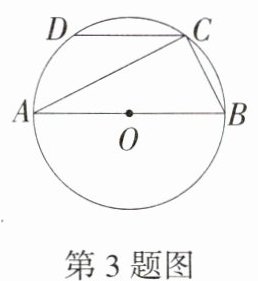

答案:
64
解析
∵CD//AB,
∴∠CAB = ∠ACD = 26°,
∵AB是⊙O的直径,
∴∠ACB = 90°,
∴∠ABC = 90° - ∠CAB = 90° - 26° = 64°.
解析
∵CD//AB,
∴∠CAB = ∠ACD = 26°,
∵AB是⊙O的直径,
∴∠ACB = 90°,
∴∠ABC = 90° - ∠CAB = 90° - 26° = 64°.
4.(2022山东日照中考)一圆形玻璃镜面损坏了一部分,为得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得AB = 12 cm,BC = 5 cm,则圆形镜面的半径为________.(M9202002)
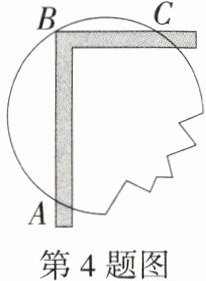

答案:
6.5 cm
解析 连接AC,
∵∠ABC = 90°,且∠ABC是圆周角,
∴AC是圆形镜面的直径,由勾股定理得AC = $\sqrt{AB^{2}+BC^{2}}$ = $\sqrt{12^{2}+5^{2}}$ = 13(cm),
∴圆形镜面的半径为6.5 cm.
解析 连接AC,
∵∠ABC = 90°,且∠ABC是圆周角,
∴AC是圆形镜面的直径,由勾股定理得AC = $\sqrt{AB^{2}+BC^{2}}$ = $\sqrt{12^{2}+5^{2}}$ = 13(cm),
∴圆形镜面的半径为6.5 cm.
5.(2024湖南师大附中芙蓉中学月考)如图,AB是⊙O的直径,弦AC = 3 cm,BC = 4 cm,CD⊥AB,垂足为点D,求CD的长.
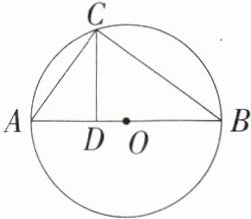

答案:
解析
∵AB是⊙O的直径,
∴∠ACB = 90°,
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{3^{2}+4^{2}}$ = 5(cm).
∵△ABC的面积 = $\frac{1}{2}$AB·CD = $\frac{1}{2}$AC·BC,
∴CD = $\frac{3×4}{5}$ = $\frac{12}{5}$(cm).
∵AB是⊙O的直径,
∴∠ACB = 90°,
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{3^{2}+4^{2}}$ = 5(cm).
∵△ABC的面积 = $\frac{1}{2}$AB·CD = $\frac{1}{2}$AC·BC,
∴CD = $\frac{3×4}{5}$ = $\frac{12}{5}$(cm).
6.(2024湖南娄底月考)如图,四边形ABCD是⊙O的内接四边形,若∠B = 135°,则∠D的度数为 ( )
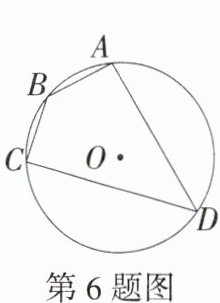
A.55°
B.45°
C.35°
D.25°

A.55°
B.45°
C.35°
D.25°
答案:
B
∵四边形ABCD是⊙O的内接四边形,∠B = 135°,
∴∠D = 180° - 135° = 45°,故选B.
∵四边形ABCD是⊙O的内接四边形,∠B = 135°,
∴∠D = 180° - 135° = 45°,故选B.
7.一题多解(2024湖南长沙天心湘郡培粹中学月考)如图,四边形ABCD内接于⊙O,AB是⊙O的直径,∠ABD = 20°,则∠BCD的度数是 ( )
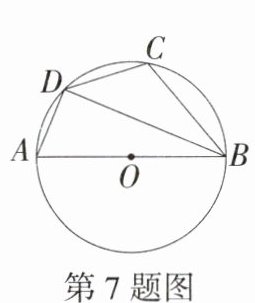
A.90°
B.100°
C.110°
D.120°

A.90°
B.100°
C.110°
D.120°
答案:
C 【解法一】
∵AB是⊙O的直径,
∴∠ADB = 90°,
∵∠ABD = 20°,
∴∠A = 70°.
∵四边形ABCD是圆内接四边形,
∴∠A + ∠BCD = 180°,
∴∠BCD = 110°,选C.
【解法二】连接OD,
∵∠ABD = 20°,
∴∠AOD = 40°,
∵OA = OD,
∴∠OAD = ∠ODA = $\frac{1}{2}$×(180° - ∠AOD) = 70°,
∵四边形ABCD是圆内接四边形,
∴∠OAD + ∠BCD = 180°,
∴∠BCD = 110°,故选C.
∵AB是⊙O的直径,
∴∠ADB = 90°,
∵∠ABD = 20°,
∴∠A = 70°.
∵四边形ABCD是圆内接四边形,
∴∠A + ∠BCD = 180°,
∴∠BCD = 110°,选C.
【解法二】连接OD,
∵∠ABD = 20°,
∴∠AOD = 40°,
∵OA = OD,
∴∠OAD = ∠ODA = $\frac{1}{2}$×(180° - ∠AOD) = 70°,
∵四边形ABCD是圆内接四边形,
∴∠OAD + ∠BCD = 180°,
∴∠BCD = 110°,故选C.
8.教材变式·P55T3 如图,四边形ABCD内接于⊙O,若它的一个外角∠DCE = 122°,则另一个外角∠DAF = _______.


答案:
58°
解析
∵∠DCE = 122°,
∴∠BCD = 180° - 122° = 58°.
∵四边形ABCD内接于⊙O,
∴∠BAD = 180° - ∠BCD = 180° - 58° = 122°,
∴∠DAF = 180° - ∠BAD = 180° - 122° = 58°.
解析
∵∠DCE = 122°,
∴∠BCD = 180° - 122° = 58°.
∵四边形ABCD内接于⊙O,
∴∠BAD = 180° - ∠BCD = 180° - 58° = 122°,
∴∠DAF = 180° - ∠BAD = 180° - 122° = 58°.
9.(2024湖南益阳大通湖二模)如图,四边形ABCD是⊙O的内接四边形,∠ADC = 2∠B,点D是$\overset{\frown}{AC}$的中点.(M9202002)
(1)求∠B的度数;
(2)求证:四边形AOCD是菱形.
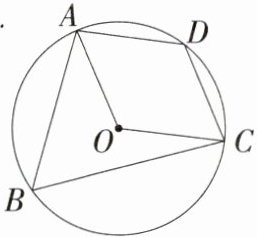
(1)求∠B的度数;
(2)求证:四边形AOCD是菱形.

答案:
解析
(1)
∵∠ADC = 2∠B,∠ADC + ∠B = 180°,
∴∠B = 60°.
(2)证明:连接OD(图略),
∵点D为$\overset{\frown}{AC}$的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{CD}$,
∴∠AOD = ∠COD,
∵∠B = 60°,
∴∠AOC = 120°,
∴∠AOD = ∠COD = 60°,
∵AO = DO = CO,
∴△AOD,△COD为等边三角形,
∴AO = CO = AD = CD,
∴四边形AOCD为菱形.
(1)
∵∠ADC = 2∠B,∠ADC + ∠B = 180°,
∴∠B = 60°.
(2)证明:连接OD(图略),
∵点D为$\overset{\frown}{AC}$的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{CD}$,
∴∠AOD = ∠COD,
∵∠B = 60°,
∴∠AOC = 120°,
∴∠AOD = ∠COD = 60°,
∵AO = DO = CO,
∴△AOD,△COD为等边三角形,
∴AO = CO = AD = CD,
∴四边形AOCD为菱形.
查看更多完整答案,请扫码查看


