《2025年5年中考3年模拟九年级数学下册湘教版》

1.（2024 湖南长沙长郡教育集团期中）在同一平面内，点P到圆上的点的最大距离为6，最小距离为4，则此圆的半径为 （ ）
A.2
B.5
C.1
D.5或1

答案： D：设此圆的半径为 $r$，当点 $P$ 在圆外时，$r = \frac{6 - 4}{2}=1$。当点 $P$ 在圆内时，$r = \frac{6 + 4}{2}=5$。综上可知，此圆的半径为 5 或 1。故选 D。

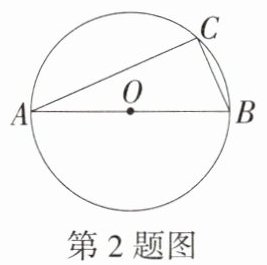
2.如图，AB为⊙O的直径，点C为⊙O上一点，且$\overset{\frown}{AC}=3\overset{\frown}{BC}$，则弦AC与弦BC的关系是 （ ）
A.$AC = 3BC$ B.$AC=\sqrt{3}BC$
C.$AC = (\sqrt{2}+1)BC$ D.$\sqrt{3}AC = BC$

答案：
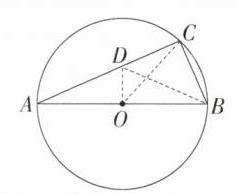
C：如图，过点 $O$ 作 $OD\perp AB$ 交 $AC$ 于点 $D$，连接 $BD$，$OC$。$\because AB$ 是 $\odot O$ 的直径，$\therefore\angle ACB = 90^{\circ}$。$\because\overset{\frown}{AC}=3\overset{\frown}{BC}$，$\therefore\angle AOC = 3\angle COB$。$\because\angle AOC+\angle COB = 180^{\circ}$，$\therefore\angle AOC = 135^{\circ}$。$\because OA = OC$，$\therefore\angle A=\angle ACO = 22.5^{\circ}$。$\because OD$ 垂直平分 $AB$，$\therefore AD = BD$，$\therefore\angle A=\angle ABD = 22.5^{\circ}$，$\therefore\angle CDB = 45^{\circ}$，$\therefore\angle CBD = 45^{\circ}$，$\therefore CD = CB$，设 $CD = CB = x$，则 $AD = BD=\sqrt{2}x$，$\therefore\frac{BC}{AC}=\frac{x}{x + \sqrt{2}x}=\frac{1}{\sqrt{2}+1}$，$\therefore AC = (\sqrt{2}+1)BC$。故选 C。

3.（2024 黑龙江大庆肇源期中）已知⊙O的半径为10 cm，AB，CD是⊙O的两条弦，$AB// CD$，$AB = 16$ cm，$CD = 12$ cm，则弦AB和弦CD之间的距离是多少？请画图并计算.（M9202003）

答案：
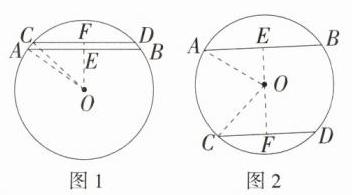
解析：有两种情况：\n①圆心 $O$ 在弦 $AB$ 和弦 $CD$ 的同旁，如图 1，连接 $OC$，$OA$，过点 $O$ 作 $OE\perp AB$ 于点 $E$，直线 $OE$ 交 $CD$ 于点 $F$，$\because AB// CD$，$\therefore OF\perp CD$，$\because OE\perp AB$，$AB = 16\ cm$，$\therefore AE = BE = 8\ cm$，同理 $CF = DF = 6\ cm$，由勾股定理得 $OE=\sqrt{OA^{2}-AE^{2}}=\sqrt{10^{2}-8^{2}} = 6(cm)$，$OF=\sqrt{OC^{2}-CF^{2}}=\sqrt{10^{2}-6^{2}} = 8(cm)$，$\therefore EF = OF - OE=2\ cm$。\n②圆心 $O$ 在弦 $AB$ 和弦 $CD$ 之间，如图 2，此时 $EF = OE + OF = 14\ cm$。
综上可知，弦 $AB$ 和弦 $CD$ 之间的距离是 2 cm 或 14 cm。

4.（2024 云南昆明三中期末）如图，AB是⊙O的弦，$\angle OAB = 20^{\circ}$，则弦AB所对的圆周角的度数为 （ ）
A.140° B.70°
C.70°或110° D.40°或140°

答案： C：$\because AO = BO$，$\angle OAB = 20^{\circ}$，$\therefore\angle OBA=\angle OAB = 20^{\circ}$，$\therefore\angle AOB = 180^{\circ}-20^{\circ}-20^{\circ}=140^{\circ}$。当弦 $AB$ 所对的圆周角的顶点在优弧 $AB$ 上时，圆周角的度数是 $140^{\circ}\div2 = 70^{\circ}$。当弦 $AB$ 所对的圆周角的顶点在劣弧 $AB$ 上时，圆周角的度数是 $180^{\circ}-70^{\circ}=110^{\circ}$。综上可知，弦 $AB$ 所对的圆周角的度数是 $70^{\circ}$或 $110^{\circ}$。故选 C。

5.（2024 江苏盐城一模）在半径为2的⊙O中，弦AB的长度2，点C为⊙O上异于A、B两点的一个动点，则$\angle BCA$的度数为________.（M9202002）

答案：
$30^{\circ}$或 $150^{\circ}$
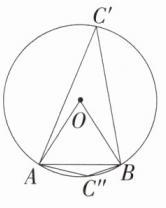
解析：如图，由题意得 $AB = OA = OB = 2$，$\therefore\triangle AOB$ 是等边三角形，$\therefore\angle AOB = 60^{\circ}$。$\because$ 点 $C$ 为 $\odot O$ 上异于 $A$、$B$ 两点的一个动点，$\therefore$ 点 $C$ 的位置有两种情况：当点 $C$ 在优弧 $AB$ 上时，$\angle AC'B=\frac{1}{2}\angle AOB = 30^{\circ}$。当点 $C$ 在劣弧 $AB$ 上时，$\because$ 四边形 $AC'BC''$ 是 $\odot O$ 的内接四边形，$\therefore\angle AC''B = 180^{\circ}-\angle AC'B = 150^{\circ}$。综上所述，$\angle BCA = 30^{\circ}$或 $150^{\circ}$。

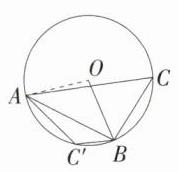
6.（2023 湖北随州随县模拟）⊙O是$\triangle ABC$的外接圆，连接OB，$\angle ABO = 38^{\circ}$，则$\angle C$的度数为______.

答案：
 $52^{\circ}$或 $128^{\circ}$
解析：如图，连接 $OA$，$\because OA = OB$，$\therefore\angle OAB=\angle ABO = 38^{\circ}$，$\therefore\angle AOB = 180^{\circ}-38^{\circ}-38^{\circ}=104^{\circ}$。当点 $C$ 在优弧 $AB$ 上时，$\angle C=\frac{1}{2}\angle AOB = 52^{\circ}$，当点 $C$ 在劣弧 $AB$ 上时，$\angle C' = 180^{\circ}-52^{\circ}=128^{\circ}$。故 $\angle C$ 的度数为 $52^{\circ}$或 $128^{\circ}$。

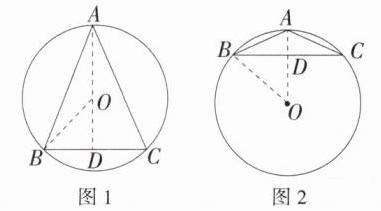
7.（2024 江苏常州天宁潭中学月考）在$\triangle ABC$中，$AB = AC$，$BC = 6$，$\triangle ABC$外接圆的半径为5，则$\triangle ABC$的面积为__________.（M9202004）

答案：
 27 或 3
解析：当 $\triangle ABC$ 是锐角三角形时，如图 1，过 $A$ 点作 $AD\perp BC$ 于点 $D$，则 $AD$ 一定经过 $\triangle ABC$ 外接圆的圆心 $O$，连接 $OB$。在 $Rt\triangle OBD$ 中，$BD=\frac{1}{2}BC=\frac{1}{2}\times6 = 3$，$\therefore OD=\sqrt{OB^{2}-BD^{2}}=\sqrt{5^{2}-3^{2}} = 4$，$\therefore AD = OA + OD = 5 + 4 = 9$，$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times6\times9 = 27$。当 $\triangle ABC$ 是钝角三角形时，如图 2，同理可得 $OD = 4$，则 $AD = OA - OD = 5 - 4 = 1$，$\therefore S_{\triangle ABC}=\frac{1}{2}BC\cdot AD=\frac{1}{2}\times6\times1 = 3$。综上可知，$\triangle ABC$ 的面积为 27 或 3。

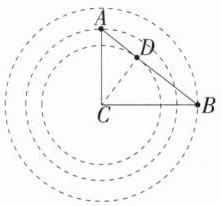
8.（2024 江苏扬州宝应期中）在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$AC = 3$，$BC = 4$，若以C点为圆心，r为半径所作的圆与斜边AB只有一个公共点，则半径r的取值范围是______________.（M9202005）

答案：
 $r = 2.4$ 或 $3\lt r\leqslant4$
解析：如图，当直线 $AB$ 和圆相切时，圆心到斜边 $AB$ 的距离（半径 $r$）为斜边 $AB$ 上的高，过点 $C$ 作 $CD\perp AB$ 于点 $D$，$\because\angle ACB = 90^{\circ}$，$AC = 3$，$BC = 4$，$\therefore AB=\sqrt{3^{2}+4^{2}} = 5$，$\therefore r = CD=\frac{AC\cdot BC}{AB}=\frac{3\times4}{5}=2.4$。当圆与直线 $AB$ 相交时，半径要大于 $AC$ 的长且不大于 $BC$ 的长，$\therefore 3\lt r\leqslant4$。综上可知，$r = 2.4$ 或 $3\lt r\leqslant4$。

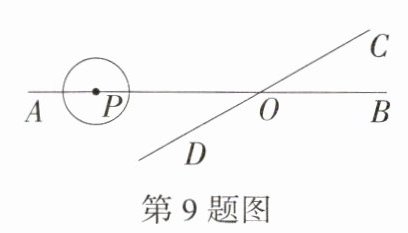
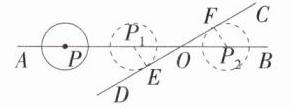
9.（2024 贵州铜仁石阡模拟）如图，直线AB，CD相交于点O，$\angle AOD = 30^{\circ}$，半径为2 cm的⊙P的圆心在直线AB上，且位于点O左侧10 cm处.若⊙P以2 cm/s的速度沿直线AB向右移动，则________后，⊙P与直线CD相切.

答案：
 3 s 或 7 s
解析：如图，$\odot P_{1}$ 在直线 $CD$ 的左侧与直线 $CD$ 相切，过点 $P_{1}$ 作 $P_{1}E\perp CD$ 于点 $E$，$\therefore P_{1}E = 2\ cm$，$\angle P_{1}EO = 90^{\circ}$。$\because\angle AOD = 30^{\circ}$，$\therefore P_{1}O = 2P_{1}E = 4\ cm$，$\therefore PP_{1}=OP - OP_{1}=10 - 4 = 6(cm)$，$\therefore\odot P$ 向右移动了 6 cm，所用的时间为 $\frac{6}{2}=3(s)$。
如图，$\odot P_{2}$ 在直线 $CD$ 的右侧与直线 $CD$ 相切，过点 $P_{2}$ 作 $P_{2}F\perp CD$ 于点 $F$，则 $P_{2}F = 2\ cm$，$\angle P_{2}FO = 90^{\circ}$，$\because\angle COB=\angle AOD = 30^{\circ}$，$\therefore P_{2}O = 2P_{2}F = 4\ cm$，$\therefore PP_{2}=OP + OP_{2}=10 + 4 = 14(cm)$，$\therefore\odot P$ 向右移动了 14 cm，所用的时间为 $\frac{14}{2}=7(s)$。
综上可知，3 s 或 7 s 后，$\odot P$ 与直线 $CD$ 相切。

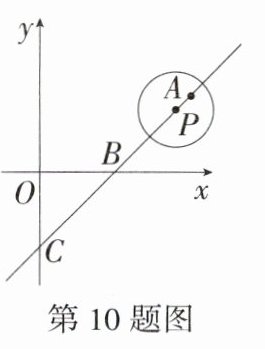
10.（2024 山东德州庆云期末）在平面直角坐标系中，直线$y = x - 2$与x轴、y轴分别交于点B、C，点$A(4,m)$也在直线上，半径为1的⊙P的圆心P从点A出发以每秒$\sqrt{2}$个单位长度沿射线AC运动，设点P运动的时间为t秒，则当t = ____________时，⊙P与坐标轴相切.

答案：
 1 或 3 或 5
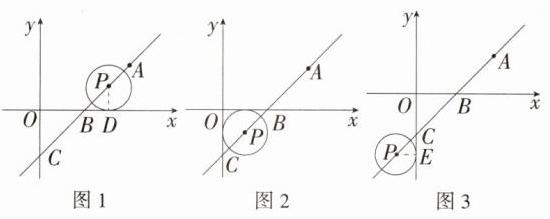
解析：对于 $y = x - 2$，当 $x = 0$ 时，$y = - 2$，当 $y = 0$ 时，$x = 2$，当 $x = 4$ 时，$y = 2$，$\therefore A(4,2)$，$B(2,0)$，$C(0,-2)$，$\therefore AB = 2\sqrt{2}$，$AC = 4\sqrt{2}$，$OB = OC = 2$，$\therefore\triangle OBC$ 是等腰直角三角形，$\angle OBC = 45^{\circ}$。\n①如图 1，$\odot P$ 只与 $x$ 轴相切，设 $\odot P$ 与坐标轴的切点为 $D$，$\because\odot P$ 的半径是 1，$\therefore PD\perp x$ 轴，$PD = 1$，$\because\angle PBD=\angle OBC = 45^{\circ}$，$\therefore\triangle BDP$ 是等腰直角三角形，$\therefore BD = PD = 1$，$\therefore PB=\sqrt{2}$，$\therefore AP = AB - PB=\sqrt{2}$，$\therefore t=\sqrt{2}\div\sqrt{2}=1$。\n②如图 2，$\odot P$ 与 $x$ 轴和 $y$ 轴都相切，$P(1,-1)$，$\therefore PB=\sqrt{2}$，$\therefore AP = AB + PB = 3\sqrt{2}$，$\therefore t = 3\sqrt{2}\div\sqrt{2}=3$。\n③如图 3，$\odot P$ 只与 $y$ 轴相切，设 $\odot P$ 与坐标轴的切点为 $E$，$\because PE = 1$，$\therefore PC=\sqrt{2}$，$\therefore AP = AC + PC = 5\sqrt{2}$，$\therefore t = 5\sqrt{2}\div\sqrt{2}=5$。
综上所述，当 $t = 1$ 或 3 或 5 时，$\odot P$ 与坐标轴相切。