第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024湖南衡阳南岳二中期未)已知一扇形的圆心角为100°,半径为9,则该扇形的弧长为 ( )
A.$\frac{45}{2}\pi$
B.5π
C.8π
D.10π
A.$\frac{45}{2}\pi$
B.5π
C.8π
D.10π
答案:
B 根据扇形的弧长公式,得该扇形的弧长为$\frac{100\pi\times9}{180}=5\pi$,故选 B.
2.(2024上海浦东新区期末)一条弧所对的圆心角是144°,那么这条弧的长与这条弧所在圆的周长的比值为(M9202006) ( )
A.$\frac{1}{3}$
B.$\frac{2}{5}$
C.$\frac{3}{4}$
D.$\frac{2}{3}$
A.$\frac{1}{3}$
B.$\frac{2}{5}$
C.$\frac{3}{4}$
D.$\frac{2}{3}$
答案:
B 设这条弧所在圆的半径为$r$,则这条弧的长为$\frac{144\pi r}{180}=\frac{4}{5}\pi r$,这条弧所在圆的周长为$2\pi r$,所以所求比值为$\frac{\frac{4}{5}\pi r}{2\pi r}=\frac{2}{5}$,故选 B.
3.(2023湖南益阳赫山一模)一个扇形的圆心角为60°,它的弧长为2π cm,则这个扇形所在圆的周长为________cm.(M9202006)
答案:
$12\pi$
解析 设这个扇形所在圆的半径为$r\ cm$,则$2\pi=\frac{60\pi r}{180}$,解得$r = 6$,$\therefore$这个扇形所在圆的周长为$2\pi\times6=12\pi(cm)$.
解析 设这个扇形所在圆的半径为$r\ cm$,则$2\pi=\frac{60\pi r}{180}$,解得$r = 6$,$\therefore$这个扇形所在圆的周长为$2\pi\times6=12\pi(cm)$.
4.新独家原创 用一根长为24 cm的细铁丝围成一个半径为6 cm的扇形,则该扇形的圆心角度数约为________.(π≈3)
答案:
$120^{\circ}$
解析 如图,$\because OA = OB = 6\ cm$,扇形的周长为$24\ cm$,$\therefore\overset{\frown}{AB}$的长为$24 - 2\times6 = 12(cm)$.设$\angle AOB = n^{\circ}$,则$\frac{n\pi\times6}{180}=12$,解得$n\approx120$,则该扇形的圆心角约为$120^{\circ}$.

$120^{\circ}$
解析 如图,$\because OA = OB = 6\ cm$,扇形的周长为$24\ cm$,$\therefore\overset{\frown}{AB}$的长为$24 - 2\times6 = 12(cm)$.设$\angle AOB = n^{\circ}$,则$\frac{n\pi\times6}{180}=12$,解得$n\approx120$,则该扇形的圆心角约为$120^{\circ}$.

5.如图,公路弯道标志$R = m$表示圆弧形道路所在圆的半径为m米,某车在标有R = 300处的弯道上从点A行驶了100π米到达点B,则线段AB = ________米.(M9202006)
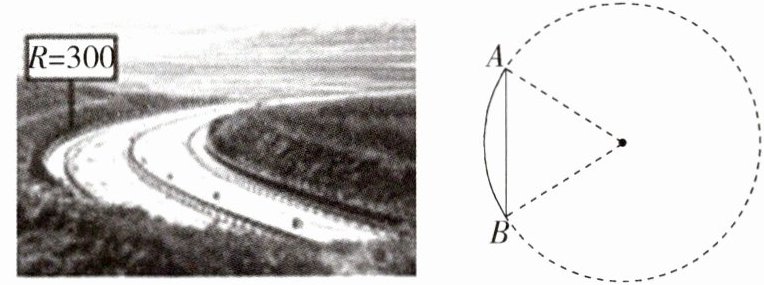

答案:
$300$
解析 如图,设弧$AB$所在圆的圆心为$O$,弧$AB$所对的圆心角的度数为$n^{\circ}$,则$100\pi=\frac{n\pi\times300}{180}$,$\therefore n = 60$,即$\angle AOB = 60^{\circ}$,又$\because AO = BO$,$\therefore\triangle AOB$是等边三角形,$\therefore AB = AO = BO = 300$米.
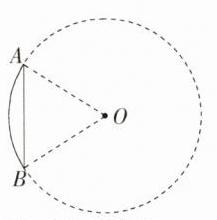
$300$
解析 如图,设弧$AB$所在圆的圆心为$O$,弧$AB$所对的圆心角的度数为$n^{\circ}$,则$100\pi=\frac{n\pi\times300}{180}$,$\therefore n = 60$,即$\angle AOB = 60^{\circ}$,又$\because AO = BO$,$\therefore\triangle AOB$是等边三角形,$\therefore AB = AO = BO = 300$米.

6.教材变式·P82T5 (2024江西赣州兴国期末)如图,$\overset{\frown}{AB}$的半径OA = 4,OC⊥AB于点C,∠AOC = 60°.求$\overset{\frown}{AB}$的长.(M9202006)


答案:
解析 $\because OC\perp AB$,$OA = OB$,$\angle AOC = 60^{\circ}$,$\therefore\angle AOB = 2\angle AOC = 120^{\circ}$,$\because OA = 4$,$\therefore\overset{\frown}{AB}$的长$=\frac{120\pi\times4}{180}=\frac{8\pi}{3}$.
7.(2023湖南张家界中考,7,★☆☆)“莱洛三角形”也称为圆弧三角形,它是工业生产中广泛使用的一种图形.如图,分别以等边△ABC的三个顶点为圆心,边长为半径画弧,三段圆弧围成的封闭图形是“莱洛三角形”.若等边△ABC的边长为3,则该“莱洛三角形”的周长等于(M9202006) ( )
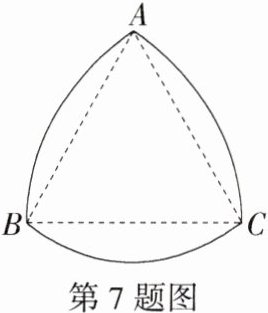
A.π
B.3π
C.2π
D.2π - $\sqrt{3}$

A.π
B.3π
C.2π
D.2π - $\sqrt{3}$
答案:
B $\because\triangle ABC$是等边三角形,$\therefore AB = BC = AC = 3$,$\angle A=\angle B = \angle C = 60^{\circ}$,$\therefore\overset{\frown}{AB}=\overset{\frown}{BC}=\overset{\frown}{AC}$,$\because\overset{\frown}{AB}$的长$=\frac{60\pi\times3}{180}=\pi$,$\therefore$该“莱洛三角形”的周长是$3\pi$.故选 B.
8.情境题·中华优秀传统文化 (2024广东东莞一模,9,★☆☆)抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.抖空竹抽象出来的图形如图所示,AC,BD分别与⊙O相切于点C,D,延长AC,BD交于点P.若∠P = 120°,⊙O的半径为6 cm,则图中$\overset{\frown}{CD}$的长为 ( )
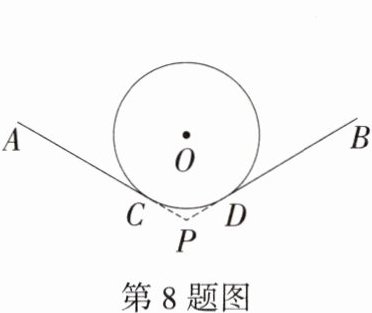
A.π cm
B.2π cm
C.3π cm
D.4π cm

A.π cm
B.2π cm
C.3π cm
D.4π cm
答案:
B 连接$OC$,$OD$,$\because AC$,$BD$分别与$\odot O$相切于点$C$,$D$,$\therefore\angle OCP=\angle ODP = 90^{\circ}$,$\therefore\angle COD = 360^{\circ}-\angle OCP-\angle ODP-\angle CPD = 360^{\circ}-90^{\circ}-90^{\circ}-120^{\circ}=60^{\circ}$,$\therefore\overset{\frown}{CD}$的长$=\frac{60\pi\times6}{180}=2\pi(cm)$.故选 B.
9.跨物理·滑轮 (2022湖南衡阳中考,17,★☆☆)如图,用一个半径为6 cm的定滑轮拉动重物上升,滑轮旋转了120°,假设绳索粗细不计,且与滑轮之间没有滑动,则重物上升了________cm.(结果保留π)(M9202006)
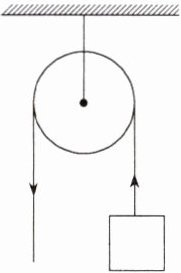

答案:
$4\pi$
解析 由题意得,重物上升的距离是半径为$6\ cm$,圆心角为$120^{\circ}$的扇形的弧长,$\therefore$重物上升的距离为$\frac{120\pi\times6}{180}=4\pi(cm)$.
解析 由题意得,重物上升的距离是半径为$6\ cm$,圆心角为$120^{\circ}$的扇形的弧长,$\therefore$重物上升的距离为$\frac{120\pi\times6}{180}=4\pi(cm)$.
10.(2024内蒙古呼伦贝尔、兴安盟中考,15,★☆☆)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,$\overset{\frown}{AB}$与$\overset{\frown}{CD}$是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC约是________米.(π取3.14,计算结果精确到0.1)
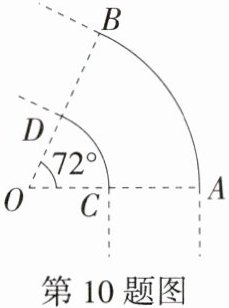

答案:
$28.7$
解析 由题意得$\frac{72\pi\cdot OA}{180}-\frac{72\pi\cdot OC}{180}=36$,$\therefore OA - OC=\frac{90}{\pi}\approx28.7$(米),$\therefore AC = OA - OC = 28.7$米,即公路宽$AC$约是$28.7$米.
解析 由题意得$\frac{72\pi\cdot OA}{180}-\frac{72\pi\cdot OC}{180}=36$,$\therefore OA - OC=\frac{90}{\pi}\approx28.7$(米),$\therefore AC = OA - OC = 28.7$米,即公路宽$AC$约是$28.7$米.
查看更多完整答案,请扫码查看


