第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024 湖南长沙长郡教育集团期中)已知一个扇形的圆心角为150°,半径是6,则这个扇形的面积是(M9202006) ( )
A.15π
B.10π
C.5π
D.2.5π
A.15π
B.10π
C.5π
D.2.5π
答案:
A:$\because$ 扇形的圆心角为 $150^{\circ}$,半径是 $6$,
$\therefore S_{扇形}=\frac{150\pi\times6^{2}}{360}=15\pi$. 故选 A.
$\therefore S_{扇形}=\frac{150\pi\times6^{2}}{360}=15\pi$. 故选 A.
2.情境题·数学文化(2024 广西南宁模拟)中国古代数学专著《九章算术》的第一章“方田”中记载了如下问题:“今有宛田,下周三十步,径十六步,问为田几何?”意思为:现有一块扇形的田,弧长是30步,其所在圆的直径是16步,则这块田的面积是(M9202006) ( )
A.200平方步
B.120平方步
C.$\frac{44\pi}{3}$平方步
D.$\frac{32\pi}{3}$平方步
A.200平方步
B.120平方步
C.$\frac{44\pi}{3}$平方步
D.$\frac{32\pi}{3}$平方步
答案:
B:$\because$ 扇形所在圆的直径是 $16$ 步,$\therefore$ 半径为 $8$ 步,
$\because$ 扇形的弧长为 $30$ 步,$\therefore S_{扇形}=\frac{1}{2}\times30\times8 = 120$(平方步). 故选 B.
$\because$ 扇形的弧长为 $30$ 步,$\therefore S_{扇形}=\frac{1}{2}\times30\times8 = 120$(平方步). 故选 B.
3.情境题·社会主义先进文化(2024 湖南邵阳邵东一模)图1是一块弘扬“社会主义核心价值观”的扇形宣传展板,该展板的部分示意图如图2所示,这两个扇形分别以点O为圆心,OA,OB的长为半径,圆心角∠O = 120°。若OA = 6 m,OB = 4 m,则阴影部分的面积为(M9202006) ( )

A.12π m²
B.$\frac{20\pi}{3}$ m²
C.8 m²
D.$\frac{16}{3}$ m²

A.12π m²
B.$\frac{20\pi}{3}$ m²
C.8 m²
D.$\frac{16}{3}$ m²
答案:
B:$S_{阴影}=S_{扇形AOD}-S_{扇形BOC}=\frac{120\pi\times6^{2}}{360}-\frac{120\pi\times4^{2}}{360}=12\pi-\frac{16\pi}{3}=\frac{20\pi}{3}(m^{2})$. 故选 B.
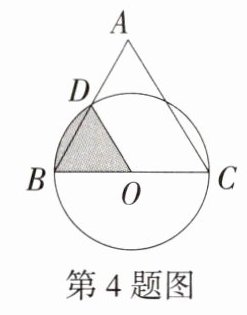
4.(2024 湖南娄底双峰模拟)如图,已知等边三角形ABC的边长为2,以边BC为直径的⊙O交AB于点D,连接OD,则阴影部分的面积是( )
A.π
B.$\frac{\pi}{3}$
C.$\frac{2\pi}{3}$
D.$\frac{\pi}{6}$

A.π
B.$\frac{\pi}{3}$
C.$\frac{2\pi}{3}$
D.$\frac{\pi}{6}$
答案:
D:$\because$ 三角形 $ABC$ 是等边三角形且边长为 $2$,
$\therefore \angle ABC = 60^{\circ}$,$OB = OC=\frac{1}{2}BC = 1$,$\because OB = OD$,
$\therefore \triangle OBD$ 是等边三角形,$\therefore \angle BOD = 60^{\circ}$,
$\therefore S_{阴影}=S_{扇形BOD}=\frac{60\pi\times1^{2}}{360}=\frac{\pi}{6}$. 故选 D.
$\therefore \angle ABC = 60^{\circ}$,$OB = OC=\frac{1}{2}BC = 1$,$\because OB = OD$,
$\therefore \triangle OBD$ 是等边三角形,$\therefore \angle BOD = 60^{\circ}$,
$\therefore S_{阴影}=S_{扇形BOD}=\frac{60\pi\times1^{2}}{360}=\frac{\pi}{6}$. 故选 D.
5.(2023 湖南永州中考)已知一个扇形的半径为6,面积为6π,则该扇形的圆心角为______°。(M9202006)
答案:
$60$
解析:设该扇形的圆心角为 $n^{\circ}$,则 $\frac{n\pi\times6^{2}}{360}=6\pi$,解得 $n = 60$,即该扇形的圆心角为 $60^{\circ}$.
解析:设该扇形的圆心角为 $n^{\circ}$,则 $\frac{n\pi\times6^{2}}{360}=6\pi$,解得 $n = 60$,即该扇形的圆心角为 $60^{\circ}$.
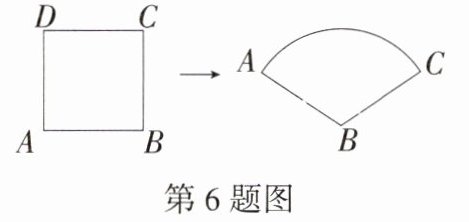
6.(2024 湖南娄底新化一模)如图,将边长为4的正方形铁丝框ABCD(面积记为S₁)变形为以点B为圆心,BC长为半径的扇形(面积记为S₂),则S₁ - S₂ = ________。(M9202006)

答案:
$0$
解析:根据题意,得 $S_{1}=4^{2}=16$,且 $\overset{\frown}{AC}$ 的长 $=AD + CD=8$,$\therefore S_{2}=\frac{1}{2}\times8\times4 = 16$,$\therefore S_{1}-S_{2}=0$.
解析:根据题意,得 $S_{1}=4^{2}=16$,且 $\overset{\frown}{AC}$ 的长 $=AD + CD=8$,$\therefore S_{2}=\frac{1}{2}\times8\times4 = 16$,$\therefore S_{1}-S_{2}=0$.
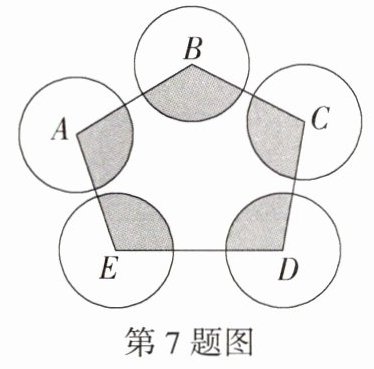
7.教材变式·P82T6 如图,分别以五边形ABCDE的各个顶点为圆心,6 cm为半径画圆,则图中阴影部分的面积为________cm²。(结果保留π)

答案:
$54\pi$
解析:由题图可知,阴影部分为 $5$ 个扇形,它们的圆心角的和等于五边形的内角和,$\because$ 五边形的内角和为 $(5 - 2)\times180^{\circ}=540^{\circ}$,$\therefore S_{阴影}=\frac{540\pi\times6^{2}}{360}=54\pi(cm^{2})$.
解析:由题图可知,阴影部分为 $5$ 个扇形,它们的圆心角的和等于五边形的内角和,$\because$ 五边形的内角和为 $(5 - 2)\times180^{\circ}=540^{\circ}$,$\therefore S_{阴影}=\frac{540\pi\times6^{2}}{360}=54\pi(cm^{2})$.
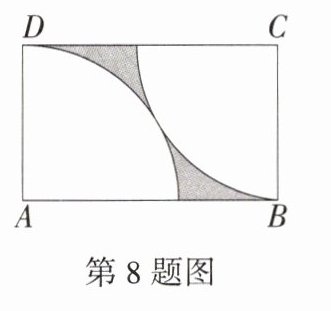
8.(2024 重庆中考A卷,8,★☆☆)如图,在矩形ABCD中,分别以点A,C为圆心,AD长为半径画弧,两弧有且仅有一个公共点。若AD = 4,则图中阴影部分的面积为(M9202006) ( )
A.32 - 8π
B.16$\sqrt{3}$ - 4π
C.32 - 4π
D.16$\sqrt{3}$ - 8π

A.32 - 8π
B.16$\sqrt{3}$ - 4π
C.32 - 4π
D.16$\sqrt{3}$ - 8π
答案:
D:如图,连接 $AC$.$\because$ 两弧有且仅有一个公共点,$AD = 4$,$\therefore AC = 2AD = 8$,在 $Rt\triangle ADC$ 中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$,
$\therefore S_{矩形ABCD}=AD\cdot CD = 16\sqrt{3}$.
$\because$ 两个扇形均为 $\frac{1}{4}$ 个圆,而且它们的半径相等,
$\therefore S_{两个扇形}=2\times\frac{1}{4}\pi\cdot AD^{2}=8\pi$,$\therefore S_{阴影}=S_{矩形ABCD}-S_{两个扇形}=16\sqrt{3}-8\pi$. 故选 D.
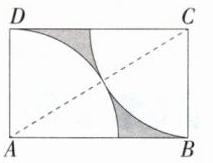
D:如图,连接 $AC$.$\because$ 两弧有且仅有一个公共点,$AD = 4$,$\therefore AC = 2AD = 8$,在 $Rt\triangle ADC$ 中,$CD=\sqrt{AC^{2}-AD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$,
$\therefore S_{矩形ABCD}=AD\cdot CD = 16\sqrt{3}$.
$\because$ 两个扇形均为 $\frac{1}{4}$ 个圆,而且它们的半径相等,
$\therefore S_{两个扇形}=2\times\frac{1}{4}\pi\cdot AD^{2}=8\pi$,$\therefore S_{阴影}=S_{矩形ABCD}-S_{两个扇形}=16\sqrt{3}-8\pi$. 故选 D.

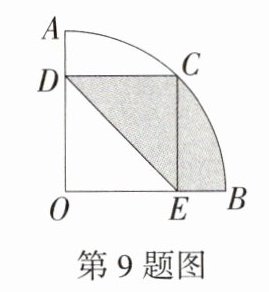
9.等积转换法(2023 四川广元中考,7,★☆☆)如图,半径为5的扇形AOB中,∠AOB = 90°,C是$\overset{\frown}{AB}$上一点,CD⊥OA,CE⊥OB,垂足分别为D,E,若CD = CE,则图中阴影部分的面积为( )
A.$\frac{25\pi}{16}$
B.$\frac{25\pi}{8}$
C.$\frac{25\pi}{6}$
D.$\frac{25\pi}{4}$

A.$\frac{25\pi}{16}$
B.$\frac{25\pi}{8}$
C.$\frac{25\pi}{6}$
D.$\frac{25\pi}{4}$
答案:
B:如图,连接 $OC$,$\because \angle AOB = 90^{\circ}$,$CD\perp OA$,$CE\perp OB$,
$\therefore \angle AOB=\angle ODC=\angle OEC = 90^{\circ}$,
$\therefore$ 四边形 $OECD$ 是矩形,
$\because CD = CE$,$\therefore$ 四边形 $OECD$ 是正方形,
$\therefore \triangle DCE\cong\triangle OEC$,$\angle COE = 45^{\circ}$,
$\therefore S_{阴影}=S_{扇形COB}=\frac{45\pi\times5^{2}}{360}=\frac{25\pi}{8}$,故选 B.
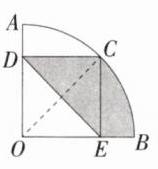
B:如图,连接 $OC$,$\because \angle AOB = 90^{\circ}$,$CD\perp OA$,$CE\perp OB$,
$\therefore \angle AOB=\angle ODC=\angle OEC = 90^{\circ}$,
$\therefore$ 四边形 $OECD$ 是矩形,
$\because CD = CE$,$\therefore$ 四边形 $OECD$ 是正方形,
$\therefore \triangle DCE\cong\triangle OEC$,$\angle COE = 45^{\circ}$,
$\therefore S_{阴影}=S_{扇形COB}=\frac{45\pi\times5^{2}}{360}=\frac{25\pi}{8}$,故选 B.

查看更多完整答案,请扫码查看


