第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2023天津河西双水道中学期末)已知一个直角三角形两直角边长度之和为20 cm,则这个直角三角形的最大面积为(M9201005)( )
A.25 cm²
B.50 cm²
C.100 cm²
D.不确定
A.25 cm²
B.50 cm²
C.100 cm²
D.不确定
答案:
B:设这个直角三角形的一条直角边长为$x cm$,面积为$S cm^{2}$,则另一条直角边长为$(20 - x) cm$,$\therefore S=\frac{1}{2}x(20 - x)=-\frac{1}{2}(x - 10)^{2}+50$,$\because-\frac{1}{2}<0$,$\therefore$当$x = 10$时,$S$取得最大值,为$50$,$\therefore$这个直角三角形的最大面积为$50 cm^{2}$。故选 B。
2.(2024安徽安庆宿松四校联考期中)如图所示的是一个长20 m、宽16 m的矩形花园,根据需要将它的长缩短
x m,宽增加x m,要想使修改后的花园面积最大,则x的值应为( )

A.1
B.1.5
C.2
D.4
x m,宽增加x m,要想使修改后的花园面积最大,则x的值应为( )

A.1
B.1.5
C.2
D.4
答案:
C:设修改后的花园面积为$S m^{2}$,则$S=(20 - x)(16 + x)=-x^{2}+4x + 320=-(x - 2)^{2}+324$,$\therefore$当$x = 2$时,$S$取得最大值,故选 C。
3.新考法(2023山西运城夏县月考)用一根长为80 cm的铁丝围成一个面积为a cm²的矩形,小亮说:“a的值可能是200.”小倩说:“a的值可能是300.”小强说:“a的值可能是400.”小英说:“a的值可能是500.”其中说法错误的是( )
A.小亮
B.小倩
C.小强
D.小英
A.小亮
B.小倩
C.小强
D.小英
答案:
D:设矩形的一边长为$x cm$,则其邻边长为$\frac{80 - 2x}{2}=(40 - x) cm$,根据题意得$a=x(40 - x)=-x^{2}+40x=-(x - 20)^{2}+400$,$\therefore a$的最大值为$400$,$\therefore$小英的说法错误。故选 D。
4.(2024湖南长沙浏阳期中)如图,四边形ABCD的两条对角线AC,BD互相垂直,AC + BD = 10,当AC = ________时,四边形ABCD的面积最大.
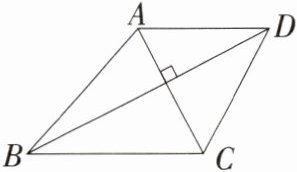

答案:
5
解析:设$AC = x$,四边形$ABCD$的面积为$S$,则$BD = 10 - x$,$\therefore S=\frac{1}{2}AC\cdot BD=\frac{1}{2}x(10 - x)=-\frac{1}{2}x^{2}+5x$,$\because-\frac{1}{2}<0$,$\therefore S$有最大值,当$x =-\frac{5}{2\times(-\frac{1}{2})}=5$时,四边形$ABCD$的面积最大,即当$AC = 5$时,四边形$ABCD$的面积最大。
解析:设$AC = x$,四边形$ABCD$的面积为$S$,则$BD = 10 - x$,$\therefore S=\frac{1}{2}AC\cdot BD=\frac{1}{2}x(10 - x)=-\frac{1}{2}x^{2}+5x$,$\because-\frac{1}{2}<0$,$\therefore S$有最大值,当$x =-\frac{5}{2\times(-\frac{1}{2})}=5$时,四边形$ABCD$的面积最大,即当$AC = 5$时,四边形$ABCD$的面积最大。
5.教材变式·P32T4(2024甘肃定西期中)在边长为6 cm的正方形ABCD中,点E,F,G,H分别按A→B,B→C,C→D,D→A的方向在正方形ABCD的边上由一个顶点向另一个顶点运动,各点同时出发,以1 cm/s的速度匀速运动.写出四边形EFGH的面积S(cm²)关于运动时间t(s)的函数关系式,并求运动几秒钟时,面积最小,最小值是多少.(M9201005)
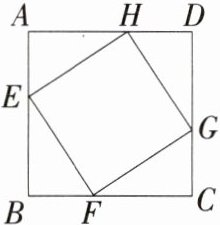

答案:
解析:由题意知$AE = t cm$,$\triangle AEH$、$\triangle BFE$、$\triangle CGF$、$\triangle DHG$全等,则$EB=(6 - t) cm$,$\therefore S = 6^{2}-\frac{1}{2}t(6 - t)\times4=2t^{2}-12t + 36=2(t - 3)^{2}+18$。$\because0\leq t\leq6$,$2>0$,$\therefore$当$t = 3$时,$S$取得最小值,为$18$。故运动$3 s$时,四边形$EFGH$的面积最小,最小值是$18 cm^{2}$。
6.情境题·劳动生产(2024湖南长沙明德教育集团期中)为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某中学准备用16米长的篱笆(如图中虚线部分)围成两面靠墙的矩形苗圃(围墙足够长).设矩形一边长为x(米),面积为y(平方米).(M9201005)
(1)求y关于x的函数解析式.
(2)当矩形苗圃面积为60平方米时,求矩形的边长.
(3)当x为何值时,所围苗圃面积最大?最大值是多少?
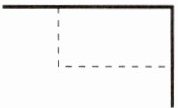
(1)求y关于x的函数解析式.
(2)当矩形苗圃面积为60平方米时,求矩形的边长.
(3)当x为何值时,所围苗圃面积最大?最大值是多少?

答案:
解析:
(1)由题意可得$y=x(16 - x)=-x^{2}+16x$,故$y$关于$x$的函数解析式为$y=-x^{2}+16x$。
(2)当$y = 60$时,$-x^{2}+16x = 60$,解得$x_{1}=6$,$x_{2}=10$,$\therefore$矩形的宽为$6$米,长为$10$米。
(3)由
(1)知$y=-x^{2}+16x=-(x - 8)^{2}+64$,$\because-1<0$,$\therefore$当$x = 8$时,$y$取得最大值,最大值为$64$,$\therefore$当$x = 8$时,所围苗圃的面积最大,最大面积是$64$平方米。
(1)由题意可得$y=x(16 - x)=-x^{2}+16x$,故$y$关于$x$的函数解析式为$y=-x^{2}+16x$。
(2)当$y = 60$时,$-x^{2}+16x = 60$,解得$x_{1}=6$,$x_{2}=10$,$\therefore$矩形的宽为$6$米,长为$10$米。
(3)由
(1)知$y=-x^{2}+16x=-(x - 8)^{2}+64$,$\because-1<0$,$\therefore$当$x = 8$时,$y$取得最大值,最大值为$64$,$\therefore$当$x = 8$时,所围苗圃的面积最大,最大面积是$64$平方米。
查看更多完整答案,请扫码查看


