第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2023山东潍坊潍城期中)下列圆中,既有圆心角又有圆周角的是(M9202001) ( )


答案:
A.图中只有圆周角,没有圆心角;B.图中只有圆心角,没有圆周角;D.图中只有圆心角,没有圆周角.故选C.
2.(2024河南漯河舞阳二模)如图,圆上依次有A,B,C,D四个点,AC,BD交于点P,连接AD,AB,BC,若∠ACB = 40°,则∠ADB的度数为 ( )

A.30°
B.40°
C.50°
D.60°

A.30°
B.40°
C.50°
D.60°
答案:
∵$\overset{\frown}{AB}=\overset{\frown}{AB}$,
∴$∠ADB = ∠ACB = 40^{\circ}$,故选B.
∵$\overset{\frown}{AB}=\overset{\frown}{AB}$,
∴$∠ADB = ∠ACB = 40^{\circ}$,故选B.
3.(2024湖南长沙期末改编)下列说法中,正确的是 ( )
A.同心圆的周长相等
B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等
D.与半径垂直的直线是圆的对称轴
A.同心圆的周长相等
B.面积相等的圆是等圆
C.相等的圆心角所对的弧相等
D.与半径垂直的直线是圆的对称轴
答案:
∵同心圆是圆心相同,半径不同的圆,
∴同心圆的周长不相等,选项A说法错误.
∵面积相等的圆的半径也相等,
∴面积相等的圆是等圆,选项B说法正确.在同圆或等圆中,相等的圆心角所对的弧相等,选项C说法错误.与半径垂直且过圆心的直线是圆的对称轴,选项D说法错误.故选B.
∵同心圆是圆心相同,半径不同的圆,
∴同心圆的周长不相等,选项A说法错误.
∵面积相等的圆的半径也相等,
∴面积相等的圆是等圆,选项B说法正确.在同圆或等圆中,相等的圆心角所对的弧相等,选项C说法错误.与半径垂直且过圆心的直线是圆的对称轴,选项D说法错误.故选B.
4.(2024山西晋城高平三模)在探究同弧所对的圆周角与圆心角的数量关系时,我们分类讨论了如图所示的三种情况,通过添加辅助线将图2、图3转化为图1,从而证明了∠BAC = $\frac{1}{2}$∠BOC,其中体现的数学思想是(M9202002) ( )


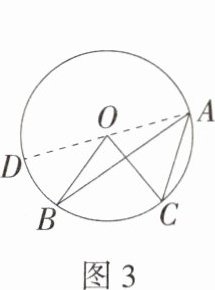
A.数形结合思想
B.转化思想
C.公理化思想
D.类比思想



A.数形结合思想
B.转化思想
C.公理化思想
D.类比思想
答案:
通过添加辅助线将题图2、题图3转化为题图1,从而证明了$∠BAC=\frac{1}{2}∠BOC$,体现的数学思想是转化思想,故选B.
5.(2024福建福州台江月考)在直角坐标系中,点P的坐标是(2,$\sqrt{2}$),☉P的半径为2,下列说法正确的是(M9202005) ( )
A.☉P与x轴、y轴都有两个公共点
B.☉P与x轴、y轴都没有公共点
C.☉P与x轴有一个公共点,与y轴有两个公共点
D.☉P与x轴有两个公共点,与y轴有一个公共点
A.☉P与x轴、y轴都有两个公共点
B.☉P与x轴、y轴都没有公共点
C.☉P与x轴有一个公共点,与y轴有两个公共点
D.☉P与x轴有两个公共点,与y轴有一个公共点
答案:
∵$P(2,\sqrt{2})$,$⊙P$的半径为2,
∴$⊙P$与x轴相交,与y轴相切,
∴$⊙P$与x轴有2个公共点,与y轴有1个公共点.故选D.
∵$P(2,\sqrt{2})$,$⊙P$的半径为2,
∴$⊙P$与x轴相交,与y轴相切,
∴$⊙P$与x轴有2个公共点,与y轴有1个公共点.故选D.
6.(2024湖南衡阳珠晖一模)如图,AB是☉O的直径,四边形ABCD内接于☉O,若BC = CD = DA = 4 cm,则☉O的直径AB为(M9202002) ( )
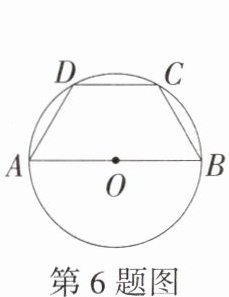
A.5 cm
B.4 cm
C.6 cm
D.8 cm

A.5 cm
B.4 cm
C.6 cm
D.8 cm
答案:
如图,连接OD,OC,
∵AB是$⊙O$的直径,$BC = CD = DA = 4\ cm$,
∴$∠AOD = ∠DOC = ∠BOC = 60^{\circ}$.又
∵$OA = OD$,
∴$\triangle AOD$是等边三角形,
∴$OA = AD = 4\ cm$,
∴$⊙O$的直径AB为8 cm.故选D.
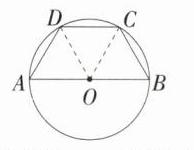
如图,连接OD,OC,
∵AB是$⊙O$的直径,$BC = CD = DA = 4\ cm$,
∴$∠AOD = ∠DOC = ∠BOC = 60^{\circ}$.又
∵$OA = OD$,
∴$\triangle AOD$是等边三角形,
∴$OA = AD = 4\ cm$,
∴$⊙O$的直径AB为8 cm.故选D.

7.(2024湖南衡阳蒸湘二模)如图,△ABC内接于☉O,AD是☉O的直径,连接CD.若∠CAD = ∠B,AD = 8,则AC的长为(M9202002) ( )
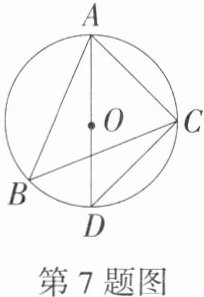
A.5
B.4$\sqrt{2}$
C.5$\sqrt{2}$
D.4$\sqrt{3}$

A.5
B.4$\sqrt{2}$
C.5$\sqrt{2}$
D.4$\sqrt{3}$
答案:
∵AD是$⊙O$的直径,
∴$∠ACD = 90^{\circ}$,
∴$∠ADC + ∠CAD = 90^{\circ}$,
∵$∠CAD = ∠B$,$∠ADC = ∠B$,
∴$∠CAD = ∠ADC = 45^{\circ}$,
∴$\triangle ACD$是等腰直角三角形,
∴$AC=\frac{AD}{\sqrt{2}}=\frac{8}{\sqrt{2}} = 4\sqrt{2}$,故选B.
∵AD是$⊙O$的直径,
∴$∠ACD = 90^{\circ}$,
∴$∠ADC + ∠CAD = 90^{\circ}$,
∵$∠CAD = ∠B$,$∠ADC = ∠B$,
∴$∠CAD = ∠ADC = 45^{\circ}$,
∴$\triangle ACD$是等腰直角三角形,
∴$AC=\frac{AD}{\sqrt{2}}=\frac{8}{\sqrt{2}} = 4\sqrt{2}$,故选B.
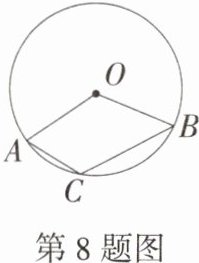
8.(2024山东聊城模拟)如图,在☉O中,点C为$\overset{\frown}{AB}$上一点,$\overset{\frown}{BC}=2\overset{\frown}{AC}$.若∠ACB = 120°,且AC是☉O的内接正n边形的一边,则n的值为 ( )
A.8
B.9
C.10
D.12

A.8
B.9
C.10
D.12
答案:
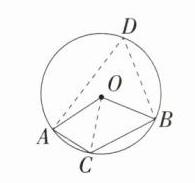
如图,连接OC,在优弧$\overset{\frown}{AB}$上任取异于A,B的一点D,连接AD,BD,
∵四边形ACBD是$⊙O$的内接四边形,
∴$∠D + ∠ACB = 180^{\circ}$,
∵$∠ACB = 120^{\circ}$,
∴$∠D = 180^{\circ}-120^{\circ}=60^{\circ}$,
∴$∠AOB = 2∠D = 120^{\circ}$.
∵$\overset{\frown}{BC}=2\overset{\frown}{AC}$,
∴$∠AOC=\frac{1}{2}∠BOC$,
∴$∠AOC=\frac{1}{3}∠AOB = 40^{\circ}$.
∵AC是$⊙O$的内接正n边形的一边,
∴$n=\frac{360^{\circ}}{40^{\circ}} = 9$.故选B.
如图,连接OC,在优弧$\overset{\frown}{AB}$上任取异于A,B的一点D,连接AD,BD,
∵四边形ACBD是$⊙O$的内接四边形,
∴$∠D + ∠ACB = 180^{\circ}$,
∵$∠ACB = 120^{\circ}$,
∴$∠D = 180^{\circ}-120^{\circ}=60^{\circ}$,
∴$∠AOB = 2∠D = 120^{\circ}$.
∵$\overset{\frown}{BC}=2\overset{\frown}{AC}$,
∴$∠AOC=\frac{1}{2}∠BOC$,
∴$∠AOC=\frac{1}{3}∠AOB = 40^{\circ}$.
∵AC是$⊙O$的内接正n边形的一边,
∴$n=\frac{360^{\circ}}{40^{\circ}} = 9$.故选B.

查看更多完整答案,请扫码查看


