《2025年5年中考3年模拟九年级数学下册湘教版》

12.(2024安徽中考,23,★★☆)已知抛物线$y=-x^{2}+bx(b$为常数)的顶点横坐标比抛物线$y=-x^{2}+2x$的顶点横坐标大1. (M9201002)
(1)求$b$的值.
(2)点$A(x_{1},y_{1})$在抛物线$y=-x^{2}+2x$上,点$B(x_{1}+t,y_{1}+h)$在抛物线$y=-x^{2}+bx$上.
(i)若$h = 3t$,且$x_{1}\geqslant0,t＞0$,求$h$的值.
(ii)若$x_{1}=t - 1$,求$h$的最大值.

答案： 解析：\n（1）$\because$抛物线$y=-x^{2}+bx$的顶点横坐标为$-\frac{b}{-2}=\frac{b}{2}$，抛物线$y=-x^{2}+2x$的顶点横坐标为$-\frac{2}{-2}=1$，$\therefore\frac{b}{2}-1 = 1$，解得$b = 4$.\n（2）$\because$点$A(x_{1},y_{1})$在抛物线$y=-x^{2}+2x$上，$\therefore y_{1}=-x_{1}^{2}+2x_{1}$.$\because$点$B(x_{1}+t,y_{1}+h)$在抛物线$y=-x^{2}+4x$上，$\therefore y_{1}+h=-(x_{1}+t)^{2}+4(x_{1}+t)$，$\therefore h=-t^{2}-2x_{1}t + 2x_{1}+4t$.\n（i）$\because h = 3t$，$\therefore 3t=-t^{2}-2x_{1}t + 2x_{1}+4t$，$\therefore t(t + 2x_{1})=t + 2x_{1}$.$\because x_{1}\geqslant0$，$t＞0$，$\therefore t + 2x_{1}＞0$，$\therefore t = 1$，$\therefore h = 3$.\n（ii）将$x_{1}=t - 1$代入$h=-t^{2}-2x_{1}t + 2x_{1}+4t$，得$h=-t^{2}-2(t - 1)t+2(t - 1)+4t=-3t^{2}+8t - 2=-3(t-\frac{4}{3})^{2}+\frac{10}{3}$.$\because - 3＜0$，$\therefore$当$t=\frac{4}{3}$，即$x_{1}=\frac{1}{3}$时，$h$取得最大值，为$\frac{10}{3}$.

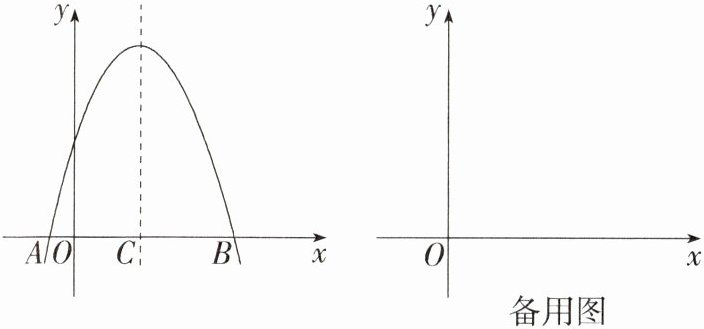
13.推理能力 (2020湖南湘潭中考)如图,抛物线$y=-x^{2}+bx + 5$与$x$轴交于$A,B$两点.
(1)若过点$C$的直线$x = 2$是抛物线的对称轴.
①求抛物线的解析式.
②对称轴上是否存在一点$P$,使点$B$关于直线$OP$的对称点$B'$恰好落在对称轴上? 若存在,请求出点$P$的坐标;若不存在,请说明理由.
(2)当$b\geqslant4,0\leqslant x\leqslant2$时,函数值$y$的最大值满足$3\leqslant y\leqslant15$,求$b$的取值范围.

答案： 解析：\n（1）①易知抛物线$y=-x^{2}+bx + 5$的对称轴为直线$x=-\frac{b}{2\times(-1)}=\frac{b}{2}$，$\because$过点$C$的直线$x = 2$是抛物线的对称轴，$\therefore\frac{b}{2}=2$，解得$b = 4$，$\therefore$抛物线的解析式为$y=-x^{2}+4x + 5$.\n②存在. 如图，点$P$在$x$轴上方，点$B$关于直线$OP$对称的点$B'$在对称轴上，连接$OB'$，$PB$，$BB'$，则$OB'=OB$，$PB'=PB$，对于$y=-x^{2}+4x + 5$，令$y = 0$，则$-x^{2}+4x + 5 = 0$，解得$x_{1}=-1$，$x_{2}=5$，$\therefore A(-1,0)$，$B(5,0)$，$\therefore OB'=OB = 5$，$\therefore CB'=\sqrt{OB'^{2}-OC^{2}}=\sqrt{25 - 4}=\sqrt{21}$，$\therefore B'(2,\sqrt{21})$，设点$P(2,m)$，由$PB'=PB$可得$\sqrt{21}-m=\sqrt{m^{2}+(5 - 2)^{2}}$，解得$m=\frac{2\sqrt{21}}{7}$，$\therefore P(2,\frac{2\sqrt{21}}{7})$. 同理，当点$P$在$x$轴下方时，$P(2,-\frac{2\sqrt{21}}{7})$. 综上所述，点$P$的坐标为$(2,\frac{2\sqrt{21}}{7})$或$(2,-\frac{2\sqrt{21}}{7})$.\n（2）抛物线$y=-x^{2}+bx + 5$的对称轴为直线$x=-\frac{b}{2\times(-1)}=\frac{b}{2}$，当$b\geqslant4$时，$\frac{b}{2}\geqslant2$，$\because$抛物线的开口向下，$\therefore$在对称轴左边，$y$随$x$的增大而增大，$\therefore$当$x = 2$时，$y$取得最大值，最大值为$-4 + 2b+5 = 2b + 1$，$\therefore 3\leqslant2b + 1\leqslant15$，解得$1\leqslant b\leqslant7$，$\because b\geqslant4$，$\therefore 4\leqslant b\leqslant7$.

例 已知某二次函数图象的一部分如图所示,当$0\leqslant x\leqslant3$时,关于该函数的函数值,下列说法正确的是 ( )


A.函数有最小值1,有最大值3
B.函数有最小值-1,有最大值0
C.函数有最小值-1,有最大值3
D.函数有最小值-1,无最大值

答案： C：由图象可知当$x = 1$时，$y$有最小值$-1$，当$x = 3$时，$y$有最大值 3，$\therefore$函数有最小值$-1$，有最大值 3，故选 C.

变式
1.变为已知函数关系式 易错题 (2023湖南长沙麓山国际实验学校第一次月考)已知二次函数$y = x^{2}-2x + 3$,当$-2\leqslant x\leqslant2$时,下列说法正确的是 (M9201002) ( )
A.有最大值11,有最小值3
B.有最大值11,有最小值2
C.有最大值3,有最小值2
D.有最大值3,有最小值1

答案： B：$\because$二次函数$y = x^{2}-2x + 3=(x - 1)^{2}+2$，$\therefore$该函数图象开口向上，对称轴是直线$x = 1$，$\because - 2\leqslant x\leqslant2$，$\therefore$当$x=-2$时，$y$取得最大值，为 11，当$x = 1$时，$y$取得最小值，为 2，故选 B.

2.二次函数表达式没有参数变为有参数 (2024四川泸州高中附属学校期中)已知关于$x$的二次函数$y = ax^{2}-4ax + a$在$-1\leqslant x\leqslant3$范围内的最大值是7,则该二次函数的最小值是__________.

答案： $-\frac{7}{2}$或$-14$
解析：抛物线$y = ax^{2}-4ax + a$的对称轴为直线$x=-\frac{-4a}{2a}=2$. 当抛物线开口向上时，$\because$二次函数在$-1\leqslant x\leqslant3$范围内的最大值为 7，$\therefore$当$x=-1$时，$y = 7$，即$7=a-4a\times(-1)+a$，解得$a=\frac{7}{6}$，当$x = 2$时，该二次函数有最小值，最小值为$\frac{7}{6}\times4-4\times\frac{7}{6}\times2+\frac{7}{6}=-\frac{7}{2}$. 当抛物线开口向下时，$\because$二次函数在$-1\leqslant x\leqslant3$范围内的最大值为 7，$\therefore$当$x = 2$时，$y = 7$，即$7 = 2^{2}a-4a\times2+a$，解得$a=-\frac{7}{3}$，当$x=-1$时，该二次函数有最小值，最小值为$-\frac{7}{3}-4\times(-\frac{7}{3})\times(-1)-\frac{7}{3}=-14$. 综上可知，该二次函数的最小值是$-\frac{7}{2}$或$-14$.