《2025年5年中考3年模拟九年级数学下册湘教版》

7.（2024天津中考，12，★☆☆）从地面竖直向上抛出一小球，小球的高度$h$（单位：m）与小球的运动时间$t$（单位：s）之间的关系式是$h = 30t - 5t^2(0\leq t\leq 6)$.有下列结论：①小球从抛出到落地需要6 s；②小球运动中的高度可以是30 m；③小球运动2 s时的高度小于运动5 s时的高度.其中，正确结论的个数是(M9201005) （ ）
A.0
B.1
C.2
D.3

答案： C 令$h = 0$，得$30t - 5t^2 = 0$，解得$t_1 = 0$，$t_2 = 6$，
∴小球从抛出到落地需要6 s，故①中结论正确.$h = 30t - 5t^2=-5(t^2 - 6t)=-5(t - 3)^2 + 45$，
∵$-5 ＜ 0$，
∴当$t = 3$时，$h$取得最大值，最大值为45，
∴小球运动中的高度可以是30 m，故②中结论正确.
∵$t = 2$时，$h = 30\times2 - 5\times2^2 = 40$（m），$t = 5$时，$h = 30\times5 - 5\times5^2 = 25$（m），$40 ＞ 25$，
∴小球运动2 s时的高度大于运动5 s时的高度，故③中结论错误. 故选C.

8.（2024广西中考，18，★☆☆）如图，壮壮同学投掷实心球，出手（点$P$处）的高度$OP$是$\frac{7}{4}$ m，出手后实心球沿一段抛物线运动，到达最高点时，水平距离是5 m，高度是4 m.若实心球落地点为$M$，则$OM$ = ________m.(M9201005)

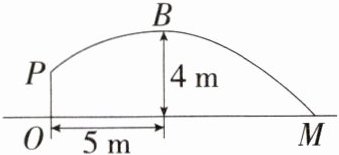
答案：
 $\frac{35}{3}$
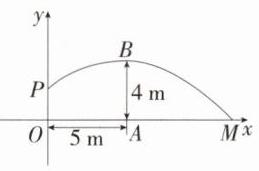
解析 如图，以O为坐标原点，直线OM为x轴，直线OP为y轴，建立直角坐标系，由题意可知$P(0,\frac{7}{4})$，$B(5,4)$，且B点为抛物线顶点，
∴可设抛物线的表达式为$y = a(x - 5)^2 + 4$，将$(0,\frac{7}{4})$代入，得$25a + 4=\frac{7}{4}$，解得$a = -\frac{9}{100}$，
∴抛物线的表达式为$y = -\frac{9}{100}(x - 5)^2 + 4$. 令$-\frac{9}{100}(x - 5)^2 + 4 = 0$，解得$x_1=\frac{35}{3}$，$x_2 = -\frac{5}{3}$（舍去），
∵M为抛物线与x轴的交点，
∴$OM=\frac{35}{3}$m.

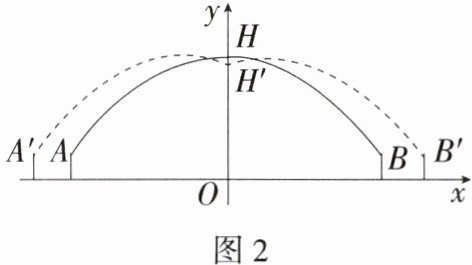
9. 情境题·劳动生产（2024湖南常德澧县期末，24，★★☆）2023年5月28日，国产大飞机C919商业首航完成，12时31分航班抵达北京首都机场，穿过隆重的“水门礼”（寓意“接风洗尘”）.如图1，两辆消防车面向飞机喷射水柱，喷射的两条水柱近似看作形状相同的抛物线的一部分.如图2，当两辆消防车喷水口$A$，$B$的水平距离为80米时，两条水柱在抛物线的顶点$H$处相遇，此时相遇点$H$距地面20米，喷水口$A$，$B$到地面的距离均为4米.若两辆消防车同时后退10米（两条水柱的形状及喷水口$A'$，$B'$到地面的距离均保持不变，按照图中所示建立平面直角坐标系），此时两条水柱相遇点$H'$距地面多少米？(M9201005)

答案： 解析 由题意可知$A(-40,4)$，$B(40,4)$，$H(0,20)$，设经过点A，B，H的抛物线的解析式为$y = ax^2 + c$，把$(0,20)$，$(-40,4)$代入$y = ax^2 + c$，得$\begin{cases}c = 20,\\1600a + c = 4,\end{cases}$解得$\begin{cases}a = -\frac{1}{100},\\c = 20,\end{cases}$
∴$y = -\frac{1}{100}x^2 + 20$.
易知经过点$B'$，$H'$的抛物线是由抛物线$y = -\frac{1}{100}x^2 + 20$向右平移10个单位得到的，
∴经过点$B'$，$H'$的抛物线的解析式为$y = -\frac{1}{100}(x - 10)^2 + 20$.
当$x = 0$时，$y = -\frac{1}{100}\times(0 - 10)^2 + 20 = 19$，
∴消防车后退10米后两条水柱相遇点$H'$地面地面19米.