第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.下列直线中,一定是圆的切线的是 ( )
A.过半径外端的直线
B.与圆心的距离等于该圆半径的直线
C.垂直于圆的半径的直线
D.与圆有公共点的直线
A.过半径外端的直线
B.与圆心的距离等于该圆半径的直线
C.垂直于圆的半径的直线
D.与圆有公共点的直线
答案:
B 过半径外端的直线不一定垂直于半径,垂直于圆的半径的直线不一定经过半径的外端,与圆有公共点的直线与圆相交或相切. 故选 B.
2.新独家原创 如图,A,B是⊙O上的点,P是OB延长线上一点,若PA = 8,PB = 4,OB = 6,则PA与⊙O的位置关系是 ( )
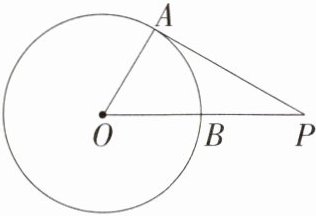
A.相切
B.相交
C.相离
D.无法确定

A.相切
B.相交
C.相离
D.无法确定
答案:
A $\because OB = 6$,$PB = 4$,$\therefore OP = 10$. 又 $\because PA = 8$,$OA = OB = 6$,$\therefore OA^{2}+AP^{2}=OP^{2}$,$\therefore\angle OAP = 90^{\circ}$,即 $OA\perp AP$,又 $\because OA$ 是 $\odot O$ 的半径,$\therefore PA$ 与 $\odot O$ 相切. 故选 A.
3.教材变式·P67T2 如图,在△OAB中,OA = OB = 5,AB = 8,⊙O的半径为3.求证:AB是⊙O的切线.(M9202005)
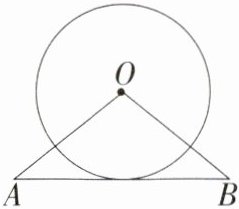

答案:
证明 过 $O$ 点作 $OC\perp AB$ 于点 $C$,$\because OA = OB$,$AB = 8$,$\therefore AC=\frac{1}{2}AB = 4$,在 $Rt\triangle OAC$ 中,$OC=\sqrt{OA^{2}-AC^{2}}=\sqrt{5^{2}-4^{2}} = 3$,$\because\odot O$ 的半径为 $3$,$\therefore OC$ 为 $\odot O$ 的半径,$\therefore AB$ 是 $\odot O$ 的切线.
4.(2023四川攀枝花中考)如图,AB为⊙O的直径,如果圆上的点D恰使∠ADC = ∠B,求证:直线CD与⊙O相切.(M9202005)
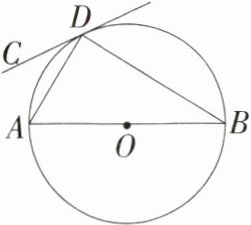

答案:
证明 连接 $OD$,$\because OA = OD$,$\therefore\angle A=\angle ODA$,$\because AB$ 为 $\odot O$ 的直径,$\therefore\angle ADB = 90^{\circ}$,$\therefore\angle A+\angle B = 90^{\circ}$,$\because\angle ADC=\angle B$,$\therefore\angle ODA+\angle ADC=\angle A+\angle B = 90^{\circ}$,即 $\angle CDO = 90^{\circ}$,$\therefore CD\perp OD$. $\because OD$ 是 $\odot O$ 的半径,$\therefore$ 直线 $CD$ 与 $\odot O$ 相切.
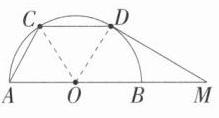
5.(2023河北邢台一模,14,★★☆)如图,已知AB是半圆O的直径,点C,D将半圆分成相等的三段弧,点M在AB的延长线上,连接MD.对于下列两个结论,判断正确的是 ( )
结论I:若∠OMD = 30°,则MD为半圆O的切线;
结论Ⅱ:连接AC,CD,则∠ACD = 130°.
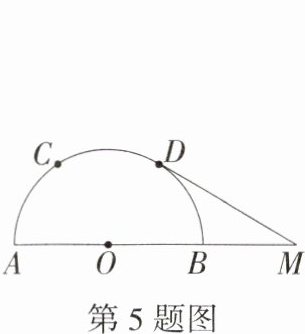
A.Ⅰ和Ⅱ都对
B.Ⅰ对、Ⅱ错
C.Ⅰ错、Ⅱ对
D.Ⅰ和Ⅱ都错
结论I:若∠OMD = 30°,则MD为半圆O的切线;
结论Ⅱ:连接AC,CD,则∠ACD = 130°.

A.Ⅰ和Ⅱ都对
B.Ⅰ对、Ⅱ错
C.Ⅰ错、Ⅱ对
D.Ⅰ和Ⅱ都错
答案:
B 如图,连接 $OD$,$OC$,$\because$ 点 $C$,$D$ 将半圆分成相等的三段弧,$\therefore\overset{\frown}{AC}=\overset{\frown}{DC}=\overset{\frown}{DB}$,$\therefore\angle AOC=\angle COD=\angle DOB=\frac{1}{3}\times180^{\circ}=60^{\circ}$. 若 $\angle OMD = 30^{\circ}$,则 $\angle ODM = 90^{\circ}$,$\therefore OD\perp DM$,$\therefore MD$ 为半圆 $O$ 的切线,故结论 Ⅰ 对. $\because OD$,$OC$,$OA$ 是半圆的半径,$\angle AOC=\angle COD = 60^{\circ}$,$\therefore\triangle AOC$,$\triangle DOC$ 是等边三角形,$\therefore\angle ACO=\angle DCO = 60^{\circ}$,$\therefore\angle ACD = 120^{\circ}$,故结论 Ⅱ 错,故选 B.
B 如图,连接 $OD$,$OC$,$\because$ 点 $C$,$D$ 将半圆分成相等的三段弧,$\therefore\overset{\frown}{AC}=\overset{\frown}{DC}=\overset{\frown}{DB}$,$\therefore\angle AOC=\angle COD=\angle DOB=\frac{1}{3}\times180^{\circ}=60^{\circ}$. 若 $\angle OMD = 30^{\circ}$,则 $\angle ODM = 90^{\circ}$,$\therefore OD\perp DM$,$\therefore MD$ 为半圆 $O$ 的切线,故结论 Ⅰ 对. $\because OD$,$OC$,$OA$ 是半圆的半径,$\angle AOC=\angle COD = 60^{\circ}$,$\therefore\triangle AOC$,$\triangle DOC$ 是等边三角形,$\therefore\angle ACO=\angle DCO = 60^{\circ}$,$\therefore\angle ACD = 120^{\circ}$,故结论 Ⅱ 错,故选 B.

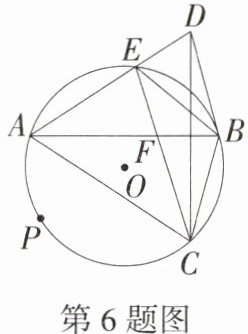
6.(2023湖南常德桃源月考,16,★★☆)如图,点P是⊙O上一点,AB是一条弦,点C是⌢APB上一点,与点D关于AB对称,AD交⊙O于点E,CE与AB交于点F,且BD//CE.给出下面四个结论:①CD平分∠BCE;②BE = BD;③AE² = AF·AB;④BD为⊙O的切线.其中所有正确结论的序号是_________.(M9202005)

答案:
①②④
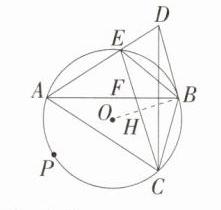
解析 $\because$ 点 $C$ 与点 $D$ 关于 $AB$ 对称,$\therefore AB$ 是 $CD$ 的垂直平分线,$\therefore AD = AC$,$BD = BC$,$\therefore\angle BCD=\angle BDC$,$\because BD// CE$,$\therefore\angle BDC=\angle DCE$,$\therefore\angle DCE=\angle BCD$,$\therefore CD$ 平分 $\angle BCE$,故①正确. $\because$ 四边形 $ACBE$ 是 $\odot O$ 的内接四边形,$\therefore\angle ACB+\angle AEB = 180^{\circ}$,$\because\angle AEB+\angle DEB = 180^{\circ}$,$\therefore\angle DEB=\angle ACB$,$\because AD = AC$,$BD = BC$,$AB = AB$,$\therefore\triangle ADB\cong\triangle ACB(SSS)$,$\therefore\angle ADB=\angle ACB$,$\therefore\angle DEB=\angle ADB$,$\therefore BD = BE$,故②正确. 对于③,若 $AE^{2}=AF\cdot AB$,则 $\frac{AE}{AB}=\frac{AF}{AE}$,再结合 $\angle BAE=\angle FAE$,可得 $\triangle AFE\backsim\triangle AEB$,但是,$\because AC\neq AE$,$\therefore\overset{\frown}{AC}\neq\overset{\frown}{AE}$,$\therefore\angle AEF\neq\angle ABE$,$\therefore\triangle AEF$ 与 $\triangle ABE$ 不相似,故③不正确. 如图,连接 $OB$,交 $EC$ 于点 $H$,$\because BD = BE$,$BD = BC$,$\therefore BE = BC$,$\therefore\overset{\frown}{BE}=\overset{\frown}{BC}$,$\therefore OB\perp CE$,$\therefore\angle OHE = 90^{\circ}$,$\because BD// CE$,$\therefore\angle OBD=\angle OHE = 90^{\circ}$,$\because OB$ 是 $\odot O$ 的半径,$\therefore BD$ 为 $\odot O$ 的切线,故④正确. 综上可知,所有正确结论的序号是①②④.
①②④
解析 $\because$ 点 $C$ 与点 $D$ 关于 $AB$ 对称,$\therefore AB$ 是 $CD$ 的垂直平分线,$\therefore AD = AC$,$BD = BC$,$\therefore\angle BCD=\angle BDC$,$\because BD// CE$,$\therefore\angle BDC=\angle DCE$,$\therefore\angle DCE=\angle BCD$,$\therefore CD$ 平分 $\angle BCE$,故①正确. $\because$ 四边形 $ACBE$ 是 $\odot O$ 的内接四边形,$\therefore\angle ACB+\angle AEB = 180^{\circ}$,$\because\angle AEB+\angle DEB = 180^{\circ}$,$\therefore\angle DEB=\angle ACB$,$\because AD = AC$,$BD = BC$,$AB = AB$,$\therefore\triangle ADB\cong\triangle ACB(SSS)$,$\therefore\angle ADB=\angle ACB$,$\therefore\angle DEB=\angle ADB$,$\therefore BD = BE$,故②正确. 对于③,若 $AE^{2}=AF\cdot AB$,则 $\frac{AE}{AB}=\frac{AF}{AE}$,再结合 $\angle BAE=\angle FAE$,可得 $\triangle AFE\backsim\triangle AEB$,但是,$\because AC\neq AE$,$\therefore\overset{\frown}{AC}\neq\overset{\frown}{AE}$,$\therefore\angle AEF\neq\angle ABE$,$\therefore\triangle AEF$ 与 $\triangle ABE$ 不相似,故③不正确. 如图,连接 $OB$,交 $EC$ 于点 $H$,$\because BD = BE$,$BD = BC$,$\therefore BE = BC$,$\therefore\overset{\frown}{BE}=\overset{\frown}{BC}$,$\therefore OB\perp CE$,$\therefore\angle OHE = 90^{\circ}$,$\because BD// CE$,$\therefore\angle OBD=\angle OHE = 90^{\circ}$,$\because OB$ 是 $\odot O$ 的半径,$\therefore BD$ 为 $\odot O$ 的切线,故④正确. 综上可知,所有正确结论的序号是①②④.

7.(2023湖南常德中考,24,★★☆)如图,四边形ABCD是⊙O的内接四边形,AB是直径,C是⌢BD的中点,过点C作CE⊥AD交AD的延长线于点E.(M9202005)
(1)求证:CE是⊙O的切线;
(2)若BC = 6,AC = 8,求CE,DE的长.
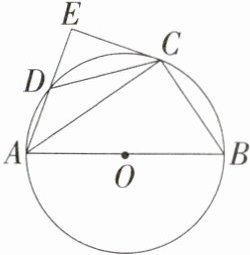
(1)求证:CE是⊙O的切线;
(2)若BC = 6,AC = 8,求CE,DE的长.

答案:
解析
(1)证明:连接 $OC$,$\because OA = OC$,$\therefore\angle OAC=\angle OCA$,$\because$ 点 $C$ 是 $\overset{\frown}{BD}$ 的中点,$\therefore\overset{\frown}{BC}=\overset{\frown}{CD}$,$\therefore\angle OAC=\angle CAE$,$\therefore\angle CAE=\angle OCA$,$\therefore OC// AE$,$\because AE\perp CE$,$\therefore OC\perp CE$,$\because OC$ 是 $\odot O$ 的半径,$\therefore CE$ 是 $\odot O$ 的切线.
(2)$\because AB$ 为 $\odot O$ 的直径,$\therefore\angle ACB = 90^{\circ}$,$\because BC = 6$,$AC = 8$,$\therefore AB=\sqrt{BC^{2}+AC^{2}} = 10$,$\because\angle CAE=\angle BAC$,$\angle AEC=\angle ACB = 90^{\circ}$,$\therefore\triangle AEC\backsim\triangle ACB$,$\therefore\frac{EC}{CB}=\frac{AC}{AB}$,即 $\frac{EC}{6}=\frac{8}{10}$,解得 $EC=\frac{24}{5}$.$\because\overset{\frown}{CD}=\overset{\frown}{BC}$,$\therefore CD = BC = 6$,$\therefore DE=\sqrt{CD^{2}-CE^{2}}=\sqrt{6^{2}-\left(\frac{24}{5}\right)^{2}}=\frac{18}{5}$.
(1)证明:连接 $OC$,$\because OA = OC$,$\therefore\angle OAC=\angle OCA$,$\because$ 点 $C$ 是 $\overset{\frown}{BD}$ 的中点,$\therefore\overset{\frown}{BC}=\overset{\frown}{CD}$,$\therefore\angle OAC=\angle CAE$,$\therefore\angle CAE=\angle OCA$,$\therefore OC// AE$,$\because AE\perp CE$,$\therefore OC\perp CE$,$\because OC$ 是 $\odot O$ 的半径,$\therefore CE$ 是 $\odot O$ 的切线.
(2)$\because AB$ 为 $\odot O$ 的直径,$\therefore\angle ACB = 90^{\circ}$,$\because BC = 6$,$AC = 8$,$\therefore AB=\sqrt{BC^{2}+AC^{2}} = 10$,$\because\angle CAE=\angle BAC$,$\angle AEC=\angle ACB = 90^{\circ}$,$\therefore\triangle AEC\backsim\triangle ACB$,$\therefore\frac{EC}{CB}=\frac{AC}{AB}$,即 $\frac{EC}{6}=\frac{8}{10}$,解得 $EC=\frac{24}{5}$.$\because\overset{\frown}{CD}=\overset{\frown}{BC}$,$\therefore CD = BC = 6$,$\therefore DE=\sqrt{CD^{2}-CE^{2}}=\sqrt{6^{2}-\left(\frac{24}{5}\right)^{2}}=\frac{18}{5}$.
查看更多完整答案,请扫码查看


