第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024福建泉州五中期中)下列图形中的角是圆心角的是 ( )
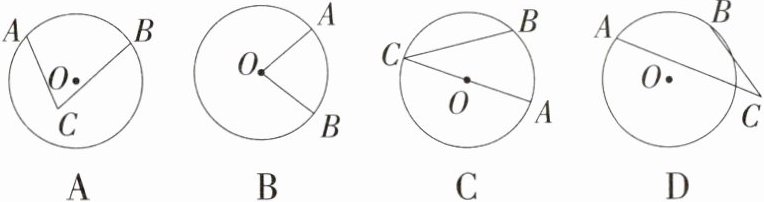

答案:
B 选项 A、C、D 中角的顶点都不是圆心,故不是圆心角. 只有选项 B 中角的顶点是圆心,是圆心角. 故选 B.
2.下列命题是真命题的是 ( )
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不相等,其所对的弦不相等
D.弦相等,它所对的圆心角相等
A.相等的弦所对的弧相等
B.圆心角相等,其所对的弦相等
C.在同圆或等圆中,圆心角不相等,其所对的弦不相等
D.弦相等,它所对的圆心角相等
答案:
C 若选项 A、B、D 中的命题是真命题,则必须以“在同圆或等圆中”为前提条件. 选项 C 中的命题是真命题,故选 C.
3.(2024湖南师大附中教育集团期中)如图,AB是⊙O的直径,$\overset{\frown}{BC}=\overset{\frown}{CD}=\overset{\frown}{DE}$,若∠COD = 35°,则∠AOE的度数是 ( )
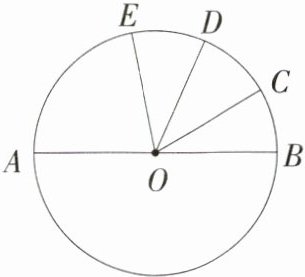
A.35°
B.55°
C.75°
D.95°

A.35°
B.55°
C.75°
D.95°
答案:
C $\because\widehat{BC}=\widehat{CD}=\widehat{DE}$,$\angle COD = 35^{\circ}$,$\therefore\angle BOC=\angle EOD=\angle COD = 35^{\circ}$,$\therefore\angle AOE = 180^{\circ}-\angle EOD-\angle COD-\angle BOC = 75^{\circ}$. 故选 C.
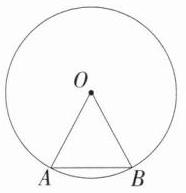
4.(2024湖南娄底双峰质检)在⊙O中,弦AB = 2 cm,圆心角∠AOB = 60°,则⊙O的直径为 ________cm.
答案:
4
解析 如图所示,在$\odot O$中,$AB = 2\ cm$,圆心角$\angle AOB = 60^{\circ}$,$OA = OB$,$\therefore\triangle OAB$是等边三角形,$\therefore OA = AB = 2\ cm$,$\therefore\odot O$的直径$= 2OA = 4\ cm$.
4
解析 如图所示,在$\odot O$中,$AB = 2\ cm$,圆心角$\angle AOB = 60^{\circ}$,$OA = OB$,$\therefore\triangle OAB$是等边三角形,$\therefore OA = AB = 2\ cm$,$\therefore\odot O$的直径$= 2OA = 4\ cm$.

5.(2024湖南长沙实验中学教育集团月考)已知弦AB把圆周分成1 : 5的两部分,则弦AB所对的圆心角的度数为 ________.
答案:
$60^{\circ}$
解析 $\because$弦$AB$把圆周分成$1:5$的两部分,$\therefore$弦$AB$所对的圆心角的度数$=360^{\circ}\times\frac{1}{1 + 5}=60^{\circ}$.
解析 $\because$弦$AB$把圆周分成$1:5$的两部分,$\therefore$弦$AB$所对的圆心角的度数$=360^{\circ}\times\frac{1}{1 + 5}=60^{\circ}$.
6.(2024天津滨海新区期末,10,★☆☆)如图,点A,B,C是⊙O上的点,∠AOC = 120°,AB = BC.若⊙O的半径为2,则四边形ABCO的面积为 ( )
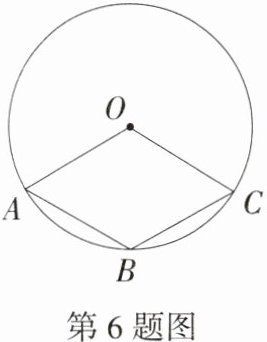
A.2$\sqrt{3}$
B.2$\sqrt{2}$
C.$\sqrt{3}$
D.2

A.2$\sqrt{3}$
B.2$\sqrt{2}$
C.$\sqrt{3}$
D.2
答案:
A 连接$OB$(图略),$\because AB = BC$,$\angle AOC = 120^{\circ}$,$\therefore\angle AOB=\angle BOC = 60^{\circ}$,又$\because OA = OC = OB$,$\therefore\triangle OAB$和$\triangle OBC$都是等边三角形,$\therefore S_{四边形 ABCO}=2\times\frac{1}{2}\times2\times(2\times\frac{\sqrt{3}}{2}) = 2\sqrt{3}$. 故选 A.
7.易错题(2024江苏宿迁洋河新区期中,14,★☆☆)如图,在同圆中,若∠AOC = 2∠BOD,则弦AC ________2BD.(填“>”“<”或“=”)
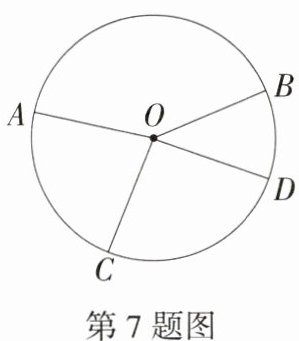

答案:
$<$
解析 如图,以$OD$为一边作$\angle DOE=\angle BOD$,$OE$与$\odot O$交于点$E$,连接$AC$、$BE$、$BD$、$ED$,则$\angle BOE = 2\angle BOD$,$BD = DE$,$\because\angle AOC = 2\angle BOD$,$\therefore\angle AOC=\angle BOE$,$\therefore AC = BE$,在$\triangle BDE$中,$BE<BD + ED = 2BD$,$\therefore AC<2BD$.
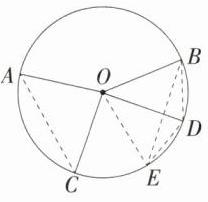
易错点 误认为弦之间的倍数关系等同于圆心角之间的倍数关系而出错.
$<$
解析 如图,以$OD$为一边作$\angle DOE=\angle BOD$,$OE$与$\odot O$交于点$E$,连接$AC$、$BE$、$BD$、$ED$,则$\angle BOE = 2\angle BOD$,$BD = DE$,$\because\angle AOC = 2\angle BOD$,$\therefore\angle AOC=\angle BOE$,$\therefore AC = BE$,在$\triangle BDE$中,$BE<BD + ED = 2BD$,$\therefore AC<2BD$.

易错点 误认为弦之间的倍数关系等同于圆心角之间的倍数关系而出错.
8.(2024浙江宁波海曙期中,20,★★☆)如图,∠AOB = 90°,C,D是$\overset{\frown}{AB}$的三等分点,连接AB分别交OC,OD于点E,F.
(1)求∠AEC的度数.
(2)求证:AE = BF = CD.
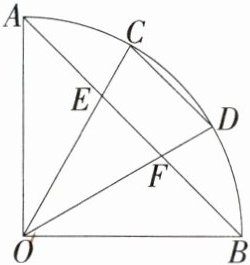
(1)求∠AEC的度数.
(2)求证:AE = BF = CD.

答案:
解析 (1)如图,连接$AC$,$DB$,$\because C$,$D$是$\widehat{AB}$的三等分点,$\therefore\widehat{AC}=\widehat{CD}=\widehat{BD}$,$\therefore AC = CD = DB$,$\angle AOC=\angle COD=\angle DOB$,$\because\angle AOB = 90^{\circ}$,$\therefore\angle AOC=\angle COD=\angle DOB = 30^{\circ}$,$\because OA = OB$,$\angle AOB = 90^{\circ}$,$\therefore\angle OAB=\angle OBA = 45^{\circ}$,$\therefore\angle AEC=\angle AOC+\angle OAB = 30^{\circ}+45^{\circ}=75^{\circ}$.
(2)证明:$\because\angle AOC = 30^{\circ}$,$OA = OC$,$\therefore\angle ACO=\frac{1}{2}(180^{\circ}-\angle AOC)=\frac{1}{2}\times(180^{\circ}-30^{\circ}) = 75^{\circ}$. 又$\because\angle AEC = 75^{\circ}$,$\therefore\angle AEC=\angle ACO$,$\therefore AE = AC$,同理可证$BF = DB$,由(1)可知$AC = CD = DB$,$\therefore AE = BF = CD$.
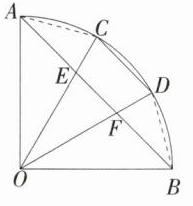
解析 (1)如图,连接$AC$,$DB$,$\because C$,$D$是$\widehat{AB}$的三等分点,$\therefore\widehat{AC}=\widehat{CD}=\widehat{BD}$,$\therefore AC = CD = DB$,$\angle AOC=\angle COD=\angle DOB$,$\because\angle AOB = 90^{\circ}$,$\therefore\angle AOC=\angle COD=\angle DOB = 30^{\circ}$,$\because OA = OB$,$\angle AOB = 90^{\circ}$,$\therefore\angle OAB=\angle OBA = 45^{\circ}$,$\therefore\angle AEC=\angle AOC+\angle OAB = 30^{\circ}+45^{\circ}=75^{\circ}$.
(2)证明:$\because\angle AOC = 30^{\circ}$,$OA = OC$,$\therefore\angle ACO=\frac{1}{2}(180^{\circ}-\angle AOC)=\frac{1}{2}\times(180^{\circ}-30^{\circ}) = 75^{\circ}$. 又$\because\angle AEC = 75^{\circ}$,$\therefore\angle AEC=\angle ACO$,$\therefore AE = AC$,同理可证$BF = DB$,由(1)可知$AC = CD = DB$,$\therefore AE = BF = CD$.

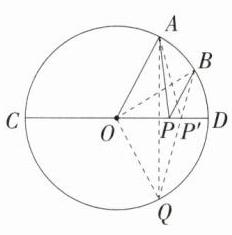
9.几何直观(2024广东云浮罗定八校联考期末)如图,点A是半圆上的一个三等分点,点B是$\overset{\frown}{AD}$的中点,P是直径CD上一动点,若⊙O的半径是2,则PA + PB的最小值为 ________.
答案:
$2\sqrt{2}$
解析 如图,作点$A$关于$CD$的对称点$Q$,连接$BQ$,交$CD$于点$P'$,点$P$在点$P'$的位置时点$P$到$A$,$B$两点的距离之和最小,最小值为$BQ$的长. 连接$OQ$,$OB$,$AP'$. $\because$点$A$和点$Q$关于$CD$对称,点$A$是半圆上的一个三等分点,$\therefore\angle DOQ=\angle AOD = 60^{\circ}$. $\because$点$B$是$\widehat{AD}$的中点,$\therefore\angle BOD = 30^{\circ}$,$\therefore\angle BOQ=\angle DOQ+\angle BOD = 90^{\circ}$,$\therefore BQ=\sqrt{OB^{2}+OQ^{2}} = 2\sqrt{2}$,即$PA + PB$的最小值为$2\sqrt{2}$.
$2\sqrt{2}$
解析 如图,作点$A$关于$CD$的对称点$Q$,连接$BQ$,交$CD$于点$P'$,点$P$在点$P'$的位置时点$P$到$A$,$B$两点的距离之和最小,最小值为$BQ$的长. 连接$OQ$,$OB$,$AP'$. $\because$点$A$和点$Q$关于$CD$对称,点$A$是半圆上的一个三等分点,$\therefore\angle DOQ=\angle AOD = 60^{\circ}$. $\because$点$B$是$\widehat{AD}$的中点,$\therefore\angle BOD = 30^{\circ}$,$\therefore\angle BOQ=\angle DOQ+\angle BOD = 90^{\circ}$,$\therefore BQ=\sqrt{OB^{2}+OQ^{2}} = 2\sqrt{2}$,即$PA + PB$的最小值为$2\sqrt{2}$.

查看更多完整答案,请扫码查看


