第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
22. [答案含评分细则]跨化学·制取氢气(2024湖南长沙开福立信中学三模)(7分)化学实验课上,张老师带来了Mg(镁)、Al(铝)、Zn(锌)、Cu(铜)四种金属,这四种金属分别用相同的不透明容器装着,让同学们随机选择一种金属与稀盐酸反应来制取氢气.(根据金属活动性顺序可知:Mg、Al、Zn可以置换出氢气,而Cu不能置换出氢气)
(1)小明从四种金属中随机选一种,则选到Al的概率为________.
(2)小明和小红分别从四种金属中随机选一种金属进行实验,求两人所选金属均能置换出氢气的概率.
(1)小明从四种金属中随机选一种,则选到Al的概率为________.
(2)小明和小红分别从四种金属中随机选一种金属进行实验,求两人所选金属均能置换出氢气的概率.
答案:
(1)$\frac{1}{4}$. …… 2 分
(2)列表如下:
| 小红 小明 | $Mg$ | $Al$ | $Zn$ | $Cu$ |
| ---- | ---- | ---- | ---- | ---- |
| $Mg$ | $(Mg,Mg)$ | $(Mg,Al)$ | $(Mg,Zn)$ | $(Mg,Cu)$ |
| $Al$ | $(Al,Mg)$ | $(Al,Al)$ | $(Al,Zn)$ | $(Al,Cu)$ |
| $Zn$ | $(Zn,Mg)$ | $(Zn,Al)$ | $(Zn,Zn)$ | $(Zn,Cu)$ |
| $Cu$ | $(Cu,Mg)$ | $(Cu,Al)$ | $(Cu,Zn)$ | $(Cu,Cu)$ |
…… 5 分
共有 16 种等可能的结果,其中两人所选金属均能置换出氢气的结果有 9 种,$\therefore$ 两人所选金属均能置换出氢气的概率为 $\frac{9}{16}$. …… 7 分
(1)$\frac{1}{4}$. …… 2 分
(2)列表如下:
| 小红 小明 | $Mg$ | $Al$ | $Zn$ | $Cu$ |
| ---- | ---- | ---- | ---- | ---- |
| $Mg$ | $(Mg,Mg)$ | $(Mg,Al)$ | $(Mg,Zn)$ | $(Mg,Cu)$ |
| $Al$ | $(Al,Mg)$ | $(Al,Al)$ | $(Al,Zn)$ | $(Al,Cu)$ |
| $Zn$ | $(Zn,Mg)$ | $(Zn,Al)$ | $(Zn,Zn)$ | $(Zn,Cu)$ |
| $Cu$ | $(Cu,Mg)$ | $(Cu,Al)$ | $(Cu,Zn)$ | $(Cu,Cu)$ |
…… 5 分
共有 16 种等可能的结果,其中两人所选金属均能置换出氢气的结果有 9 种,$\therefore$ 两人所选金属均能置换出氢气的概率为 $\frac{9}{16}$. …… 7 分
23. [答案含评分细则](2024山东滨州中考)(9分)春节期间,全国各影院上映多部影片,某影院每天运营成本为2 000元,该影院每天售出的电影票数量y(单位:张)与售价x(单位:元/张)之间满足一次函数关系(30≤x≤80,且x是整数),部分数据如下表所示:(M9201005)
|电影票售价x(元/张)|40|50|
|----|----|----|
|售出电影票数量y(张)|164|124|
(1)请求出y与x之间的函数关系式.
(2)设该影院每天的利润(利润 = 票房收入 - 运营成本)为w(单位:元),求w与x之间的函数关系式.
(3)该影院将电影票售价定为多少时,每天获利最大?最大利润是多少?
|电影票售价x(元/张)|40|50|
|----|----|----|
|售出电影票数量y(张)|164|124|
(1)请求出y与x之间的函数关系式.
(2)设该影院每天的利润(利润 = 票房收入 - 运营成本)为w(单位:元),求w与x之间的函数关系式.
(3)该影院将电影票售价定为多少时,每天获利最大?最大利润是多少?
答案:
(1)设 $y$ 与 $x$ 之间的函数关系式是 $y = kx + b(k\neq0)$,…… 1 分
将 $x = 40$,$y = 164$ 和 $x = 50$,$y = 124$ 代入解析式,得 $\begin{cases}40k + b = 164\\50k + b = 124\end{cases}$,解得 $\begin{cases}k = -4\\b = 324\end{cases}$,故 $y$ 与 $x$ 之间的函数关系式是 $y = -4x + 324(30\leqslant x\leqslant80$,且 $x$ 是整数$)$. …… 3 分
(2)$w = x(-4x + 324) - 2000 = -4x^2 + 324x - 2000(30\leqslant x\leqslant80)$. …… 5 分
(3)由
(2)知 $w = -4x^2 + 324x - 2000 = -4(x - 40.5)^2 + 4561$,…… 7 分
$\because 30\leqslant x\leqslant80$,且 $x$ 是整数,$\therefore$ 当 $x = 40$ 或 41 时,$w$ 取得最大值,此时 $w = 4560$.
答:该影院将电影票售价定为 40 元/张或 41 元/张时,每天获利最大,最大利润是 4560 元. …… 9 分
(1)设 $y$ 与 $x$ 之间的函数关系式是 $y = kx + b(k\neq0)$,…… 1 分
将 $x = 40$,$y = 164$ 和 $x = 50$,$y = 124$ 代入解析式,得 $\begin{cases}40k + b = 164\\50k + b = 124\end{cases}$,解得 $\begin{cases}k = -4\\b = 324\end{cases}$,故 $y$ 与 $x$ 之间的函数关系式是 $y = -4x + 324(30\leqslant x\leqslant80$,且 $x$ 是整数$)$. …… 3 分
(2)$w = x(-4x + 324) - 2000 = -4x^2 + 324x - 2000(30\leqslant x\leqslant80)$. …… 5 分
(3)由
(2)知 $w = -4x^2 + 324x - 2000 = -4(x - 40.5)^2 + 4561$,…… 7 分
$\because 30\leqslant x\leqslant80$,且 $x$ 是整数,$\therefore$ 当 $x = 40$ 或 41 时,$w$ 取得最大值,此时 $w = 4560$.
答:该影院将电影票售价定为 40 元/张或 41 元/张时,每天获利最大,最大利润是 4560 元. …… 9 分
24. [答案含评分细则]新考向·项目式学习试题(2024山西中考)(9分)【阅读与思考】
下面是博学小组研究性学习报告的部分内容,请认真阅读,并完成相应任务.
关于“等边半正多边形”的研究报告
博学小组
研究对象:等边半正多边形.
研究思路:类比三角形、四边形,按“概念—性质—判定”的路径,由一般到特殊进行研究.
研究方法:观察(测量、实验)—猜想—推理证明.
研究内容:
【一般概念】对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.
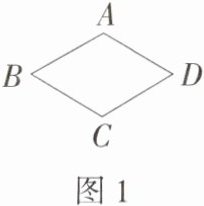
如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形……
【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:
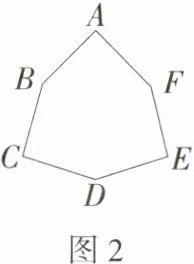
概念理解:如图2,如果六边形ABCDEF是等边半正六边形,那么AB = BC = CD = DE = EF = FA,∠A = ∠C = ∠E,∠B = ∠D = ∠F,且∠A≠∠B.
性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
内角:等边半正六边形相邻两个内角的和为 ▲ °.
对角线:……
任务:(M9202007)
(1)直接写出研究报告中“▲”处空缺的内容:________.
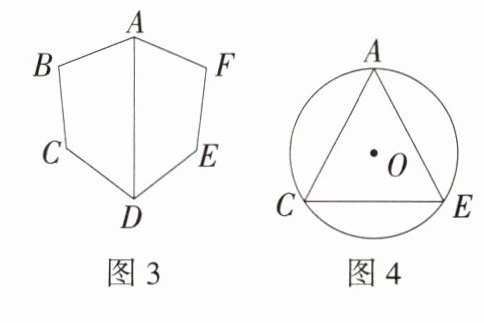
(2)如图3,六边形ABCDEF是等边半正六边形,连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
(3)如图4,已知△ACE是正三角形,⊙O是它的外接圆.请在图4中作一个等边半正六边形ABCDEF.(要求:尺规作图,保留作图痕迹,不写作法)
下面是博学小组研究性学习报告的部分内容,请认真阅读,并完成相应任务.
关于“等边半正多边形”的研究报告
博学小组
研究对象:等边半正多边形.
研究思路:类比三角形、四边形,按“概念—性质—判定”的路径,由一般到特殊进行研究.
研究方法:观察(测量、实验)—猜想—推理证明.
研究内容:
【一般概念】对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形.
如图1,我们学习过的菱形(正方形除外)就是等边半正四边形,类似地,还有等边半正六边形、等边半正八边形……

【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下:
概念理解:如图2,如果六边形ABCDEF是等边半正六边形,那么AB = BC = CD = DE = EF = FA,∠A = ∠C = ∠E,∠B = ∠D = ∠F,且∠A≠∠B.

性质探索:根据定义,探索等边半正六边形的性质,得到如下结论:
内角:等边半正六边形相邻两个内角的和为 ▲ °.
对角线:……
任务:(M9202007)
(1)直接写出研究报告中“▲”处空缺的内容:________.
(2)如图3,六边形ABCDEF是等边半正六边形,连接对角线AD,猜想∠BAD与∠FAD的数量关系,并说明理由.
(3)如图4,已知△ACE是正三角形,⊙O是它的外接圆.请在图4中作一个等边半正六边形ABCDEF.(要求:尺规作图,保留作图痕迹,不写作法)

答案:
(1)240. …… 2 分
(2)$\angle BAD = \angle FAD$. …… 3 分
理由:连接 $BD$,$FD$(图略). …… 4 分
$\because$ 六边形 $ABCDEF$ 是等边半正六边形,
$\therefore AB = BC = CD = DE = EF = FA$,$\angle C = \angle E$. …… 5 分
$\therefore \triangle BCD\cong\triangle FED(SAS)$,$\therefore BD = FD$,…… 6 分
$\therefore \triangle BAD\cong\triangle FAD(SSS)$,$\therefore \angle BAD = \angle FAD$. …… 7 分
(3)答案不唯一,例如:
【作法一】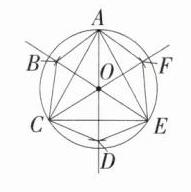
【作法二】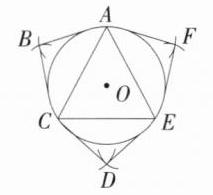
如图,六边形 $ABCDEF$ 即为所求.(评分说明:作图正确并保留作图痕迹得 1 分. 字母标注正确得 1 分)
…… 9 分
(1)240. …… 2 分
(2)$\angle BAD = \angle FAD$. …… 3 分
理由:连接 $BD$,$FD$(图略). …… 4 分
$\because$ 六边形 $ABCDEF$ 是等边半正六边形,
$\therefore AB = BC = CD = DE = EF = FA$,$\angle C = \angle E$. …… 5 分
$\therefore \triangle BCD\cong\triangle FED(SAS)$,$\therefore BD = FD$,…… 6 分
$\therefore \triangle BAD\cong\triangle FAD(SSS)$,$\therefore \angle BAD = \angle FAD$. …… 7 分
(3)答案不唯一,例如:
【作法一】

【作法二】

如图,六边形 $ABCDEF$ 即为所求.(评分说明:作图正确并保留作图痕迹得 1 分. 字母标注正确得 1 分)
…… 9 分
查看更多完整答案,请扫码查看


