第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024广东汕头下蓬中学一模)下列说法不正确的是(M9203002) ( )
A.长方体是四棱柱
B.八棱柱有16条棱
C.五棱柱有7个面
D.直棱柱的每个侧面都是长方形
A.长方体是四棱柱
B.八棱柱有16条棱
C.五棱柱有7个面
D.直棱柱的每个侧面都是长方形
答案:
B 八棱柱有 $8×3 = 24$ 条棱,选项 B 说法错误。
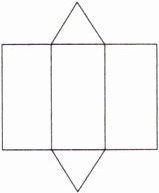
2.(2024江苏扬州中考)如图所示的是某几何体的表面展开图,则该几何体是(M9203002) ( )
A.三棱锥
B.圆锥
C.三棱柱
D.长方体

A.三棱锥
B.圆锥
C.三棱柱
D.长方体
答案:
C 由几何体的表面展开图可知,原几何体的侧面为三个相同的长方形,上、下底面为全等的三角形,符合三棱柱的特征,所以该几何体是三棱柱。故选 C。
3.新独家原创 一个直四棱柱的底面是菱形,其侧面积是60,若菱形的边长为5,则该直四棱柱所有棱长之和为________.
答案:
$52$
解析 :$\because$ 直四棱柱的侧面积是 $60$,底面是边长为 $5$ 的菱形,$\therefore$ 该直四棱柱的侧棱长为 $\frac{60}{5×4}=3$,$\therefore$ 该直四棱柱所有棱长之和为 $3×4 + 5×4×2 = 52$。
解析 :$\because$ 直四棱柱的侧面积是 $60$,底面是边长为 $5$ 的菱形,$\therefore$ 该直四棱柱的侧棱长为 $\frac{60}{5×4}=3$,$\therefore$ 该直四棱柱所有棱长之和为 $3×4 + 5×4×2 = 52$。
4.教材变式·P102例1 (2023江西九江湖口期中)如图所示的是一个食品包装盒的表面展开图,其底面为正六边形.(M9203002)
(1)请写出这个包装盒的几何体名称,并画出它的直观图;
(2)请根据图中所示的尺寸,计算这个几何体包装盒的侧面积.
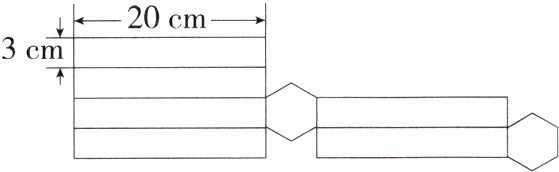
(1)请写出这个包装盒的几何体名称,并画出它的直观图;
(2)请根据图中所示的尺寸,计算这个几何体包装盒的侧面积.

答案:
解析 \n(1)这个包装盒为正六棱柱,其直观图如图所示。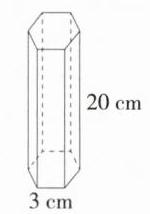
\n(2)$S_{侧}=6×3×20 = 360(cm^{2})$。
解析 \n(1)这个包装盒为正六棱柱,其直观图如图所示。

\n(2)$S_{侧}=6×3×20 = 360(cm^{2})$。
5.(2023湖南永州零陵模拟)某圆锥的底面半径是1,则该圆锥的侧面展开图中扇形的弧长为(M9203002) ( )
A.π
B.2π
C.3π
D.4π
A.π
B.2π
C.3π
D.4π
答案:
B $\because$ 圆锥的底面半径是 $1$,$\therefore$ 圆锥的底面周长是 $2\pi$,$\therefore$ 该圆锥的侧面展开图中扇形的弧长为 $2\pi$,故选 B。
6.(2024湖南长沙浏阳期中)若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为 ( )
A.15
B.12π
C.15π
D.30π
A.15
B.12π
C.15π
D.30π
答案:
C $\because$ 圆锥的底面半径为 $3$,母线长为 $5$,$\therefore$ 这个圆锥的侧面积为 $\frac{1}{2}×(2\pi×3)×5 = 15\pi$。故选 C。
7.(2023云南中考)数学活动课上,某同学制作了一顶圆锥形纸帽.若圆锥的底面半径为1分米,母线长为4分米,则该圆锥的高为________分米.
答案:
$\sqrt{15}$
解析 :由勾股定理得圆锥的高为 $\sqrt{4^{2}-1^{2}}=\sqrt{15}$(分米)。
解析 :由勾股定理得圆锥的高为 $\sqrt{4^{2}-1^{2}}=\sqrt{15}$(分米)。
8.教材变式·P104T3 已知一个圆锥的侧面展开图是一个半径为9 cm,圆心角为120°的扇形.
(1)求该圆锥的底面半径.
(2)求该圆锥的表面积.
(1)求该圆锥的底面半径.
(2)求该圆锥的表面积.
答案:
解析 \n(1)设该圆锥的底面半径为 $r\ cm$,根据题意得 $2\pi r=\frac{120\pi×9}{180}$,解得 $r = 3$,$\therefore$ 该圆锥的底面半径为 $3\ cm$。\n(2)该圆锥的侧面积为 $\frac{120\pi×9^{2}}{360}=27\pi(cm^{2})$,该圆锥的底面积为 $\pi×3^{2}=9\pi(cm^{2})$,$\therefore$ 该圆锥的表面积 $=27\pi + 9\pi = 36\pi(cm^{2})$。
9.(2023江苏无锡中考,14,★☆☆)若直三棱柱的上、下底面为正三角形,侧面展开图是边长为6的正方形,则该直三棱柱的表面积为__________.(M9203002)
答案:
$36 + 2\sqrt{3}$
解析 :由题意可知,直三棱柱的上、下底面的正三角形的边长为 $6÷3 = 2$,$\therefore$ 上、下底面的面积和为 $\frac{1}{2}×2×\sqrt{2^{2}-1^{2}}×2 = 2\sqrt{3}$。$\because$ 侧面展开图是边长为 $6$ 的正方形,$\therefore$ 直三棱柱的侧面积为 $6×6 = 36$,$\therefore$ 该直三棱柱的表面积为 $36 + 2\sqrt{3}$。
解析 :由题意可知,直三棱柱的上、下底面的正三角形的边长为 $6÷3 = 2$,$\therefore$ 上、下底面的面积和为 $\frac{1}{2}×2×\sqrt{2^{2}-1^{2}}×2 = 2\sqrt{3}$。$\because$ 侧面展开图是边长为 $6$ 的正方形,$\therefore$ 直三棱柱的侧面积为 $6×6 = 36$,$\therefore$ 该直三棱柱的表面积为 $36 + 2\sqrt{3}$。
10.(2024黑龙江龙东地区中考,17,★☆☆)若圆锥的底面半径为3,侧面积为36π,则这个圆锥的侧面展开图的圆心角是________°.(M9203002)
答案:
$90$
解析 :设圆锥的母线长为 $l$,圆锥侧面展开图的圆心角是 $n^{\circ}$。$\because$ 圆锥的侧面积为 $36\pi$,$\therefore\pi×3×l = 36\pi$,解得 $l = 12$,$\therefore36\pi=\frac{n\pi×12^{2}}{360}$,解得 $n = 90$,即圆锥侧面展开图的圆心角是 $90^{\circ}$。
解析 :设圆锥的母线长为 $l$,圆锥侧面展开图的圆心角是 $n^{\circ}$。$\because$ 圆锥的侧面积为 $36\pi$,$\therefore\pi×3×l = 36\pi$,解得 $l = 12$,$\therefore36\pi=\frac{n\pi×12^{2}}{360}$,解得 $n = 90$,即圆锥侧面展开图的圆心角是 $90^{\circ}$。
查看更多完整答案,请扫码查看


