第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
11.(2023 湖南衡阳中考,18,★★☆)用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置. 要完成这一圆环排列,共需要正五边形的个数是________。(M9202007)


答案:
$10$
解析:正五边形的每一个内角为 $\frac{1}{5}\times180^{\circ}\times(5 - 2)=108^{\circ}$,$\therefore \angle O = 180^{\circ}-(180^{\circ}-108^{\circ})\times2=36^{\circ}$,$\therefore$ 需要正五边形的个数是 $360^{\circ}\div36^{\circ}=10$.
解析:正五边形的每一个内角为 $\frac{1}{5}\times180^{\circ}\times(5 - 2)=108^{\circ}$,$\therefore \angle O = 180^{\circ}-(180^{\circ}-108^{\circ})\times2=36^{\circ}$,$\therefore$ 需要正五边形的个数是 $360^{\circ}\div36^{\circ}=10$.
12.跨艺术·园林设计(2024 江苏苏州中考,14,★★☆)铁艺花窗是园林设计中常见的装饰元素. 如图所示的是一个花瓣造型的花窗示意图,该花窗由六条等弧连接而成,六条弧所对应的弦构成一个正六边形,中心为点O,$\overset{\frown}{AB}$所在圆的圆心C恰好是△ABO的内心,若AB = 2$\sqrt{3}$,则花窗的周长(图中实线部分的长度)= ________。(结果保留π)(M9202007)
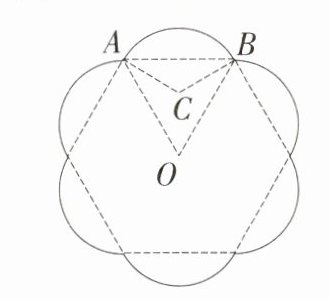

答案:
$8\pi$
解析:如图,过点 $C$ 作 $CM\perp AB$ 于点 $M$,则 $AM = BM=\frac{1}{2}AB=\sqrt{3}$,
$\because$ 六条等弧所对应的弦构成一个正六边形,中心为点 $O$,$\therefore \angle AOB = 60^{\circ}$,$\because OA = OB$,$\therefore \triangle AOB$ 是等边三角形,$\because$ 点 $C$ 是等边 $\triangle AOB$ 的内心,$\therefore \angle CAB=\angle CBA=\frac{1}{2}\times60^{\circ}=30^{\circ}$,$\angle ACB = 2\angle AOB = 120^{\circ}$,在 $Rt\triangle ACM$ 中,$AM=\sqrt{3}$,$\angle CAM = 30^{\circ}$,$\therefore AC=\frac{AM}{\cos30^{\circ}}=2$,$\because \overset{\frown}{AB}$ 的长为 $\frac{120\pi\times2}{180}=\frac{4\pi}{3}$,$\therefore$ 花窗的周长为 $\frac{4\pi}{3}\times6 = 8\pi$.
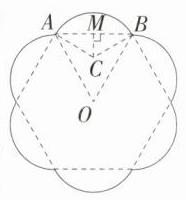
$8\pi$
解析:如图,过点 $C$ 作 $CM\perp AB$ 于点 $M$,则 $AM = BM=\frac{1}{2}AB=\sqrt{3}$,
$\because$ 六条等弧所对应的弦构成一个正六边形,中心为点 $O$,$\therefore \angle AOB = 60^{\circ}$,$\because OA = OB$,$\therefore \triangle AOB$ 是等边三角形,$\because$ 点 $C$ 是等边 $\triangle AOB$ 的内心,$\therefore \angle CAB=\angle CBA=\frac{1}{2}\times60^{\circ}=30^{\circ}$,$\angle ACB = 2\angle AOB = 120^{\circ}$,在 $Rt\triangle ACM$ 中,$AM=\sqrt{3}$,$\angle CAM = 30^{\circ}$,$\therefore AC=\frac{AM}{\cos30^{\circ}}=2$,$\because \overset{\frown}{AB}$ 的长为 $\frac{120\pi\times2}{180}=\frac{4\pi}{3}$,$\therefore$ 花窗的周长为 $\frac{4\pi}{3}\times6 = 8\pi$.

13.情境题·中华优秀传统文化(2024 甘肃武威中考,20,★★☆)马家窑文化以发达的彩陶著称于世,其陶质坚固,器表细腻,红、白、黑彩共用,彩绘线条流畅细致,图案繁缛多变,形成了绚丽典雅的艺术风格,创造了一大批令人惊叹的彩陶艺术精品,体现了古代劳动人民的智慧. 如图1所示的是彩陶纹样呈现的是三等分圆周,古人用等边三角形三点定位的方法确定圆周的三等分点,这种方法和下面三等分圆周的方法相通.
如图2,已知⊙O和圆上一点M. 作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分。(M9202007)
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2 cm,则△ABC的周长为________cm。
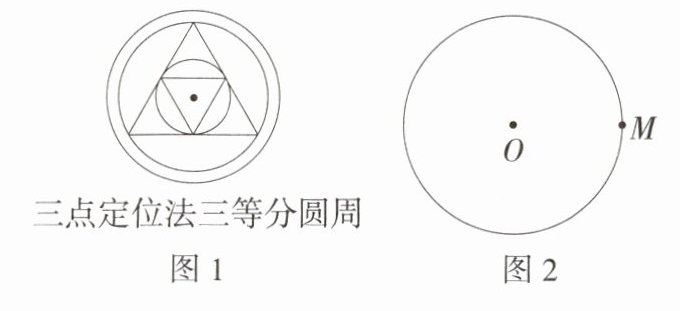
如图2,已知⊙O和圆上一点M. 作法如下:
①以点M为圆心,OM长为半径,作弧交⊙O于A,B两点;
②延长MO交⊙O于点C;
即点A,B,C将⊙O的圆周三等分。(M9202007)
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图2中将⊙O的圆周三等分(保留作图痕迹,不写作法);
(2)根据(1)画出的图形,连接AB,AC,BC,若⊙O的半径为2 cm,则△ABC的周长为________cm。

答案:
解析:
(1) 如图,点 $A$,$B$,$C$ 即为所求.
(2)$6\sqrt{3}$.
详解:如图,连接 $OA$,$OB$,$MC$ 交 $AB$ 于点 $E$.
$\because \overset{\frown}{AB}=\overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore AB = AC = CB$,$\angle AOB = 120^{\circ}$.
$\because \overset{\frown}{AM}=\overset{\frown}{BM}$,$\therefore \angle AOM=\angle BOM = 60^{\circ}$,$OE\perp AB$,
$\therefore AE = EB = AO\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}(cm)$,
$\therefore AB = 2\sqrt{3}cm$,$\therefore \triangle ABC$ 的周长为 $6\sqrt{3}cm$.
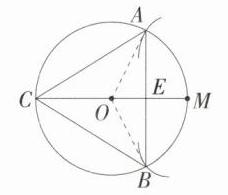
解析:
(1) 如图,点 $A$,$B$,$C$ 即为所求.
(2)$6\sqrt{3}$.
详解:如图,连接 $OA$,$OB$,$MC$ 交 $AB$ 于点 $E$.
$\because \overset{\frown}{AB}=\overset{\frown}{AC}=\overset{\frown}{BC}$,$\therefore AB = AC = CB$,$\angle AOB = 120^{\circ}$.
$\because \overset{\frown}{AM}=\overset{\frown}{BM}$,$\therefore \angle AOM=\angle BOM = 60^{\circ}$,$OE\perp AB$,
$\therefore AE = EB = AO\cdot\sin60^{\circ}=2\times\frac{\sqrt{3}}{2}=\sqrt{3}(cm)$,
$\therefore AB = 2\sqrt{3}cm$,$\therefore \triangle ABC$ 的周长为 $6\sqrt{3}cm$.

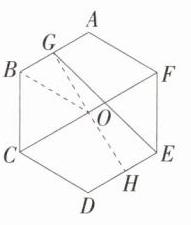
14.运算能力(2024 湖南长沙岳麓三模)雪花是一种美丽的结晶体,其形状我们可近似看作是一个正六边形ABCDEF(如图所示),连接CF,若G是AB边的中点,连接GE,则$\frac{GE}{CF}$的值为________。


答案:
$\frac{\sqrt{13}}{4}$
解析:如图,取 $DE$ 的中点 $H$,连接 $GH$,由对称性可知,$GH$ 所在的直线是正六边形的对称轴,设圆心为 $O$,连接 $OB$,$O$ 是线段 $CF$ 的中点,$\because$ 六边形 $ABCDEF$ 是正六边形,点 $O$ 是中心,$\therefore \angle BOC=\frac{360^{\circ}}{6}=60^{\circ}$,$\because OB = OC$,$\therefore \triangle BOC$ 是等边三角形,$\therefore OB = OC = BC$,在 $Rt\triangle BOG$ 中,$\angle BOG = 90^{\circ}-60^{\circ}=30^{\circ}$,设 $BG = x$,则 $OB = 2x$,$\therefore OG=\sqrt{OB^{2}-BG^{2}}=\sqrt{3}x$,$\therefore GH = 2OG = 2\sqrt{3}x$,在 $Rt\triangle EGH$ 中,$HE = x$,$GH = 2\sqrt{3}x$,$\therefore GE=\sqrt{GH^{2}+EH^{2}}=\sqrt{13}x$,
$\because CF = 2OB = 4x$,$\therefore \frac{GE}{CF}=\frac{\sqrt{13}}{4}$.
$\frac{\sqrt{13}}{4}$
解析:如图,取 $DE$ 的中点 $H$,连接 $GH$,由对称性可知,$GH$ 所在的直线是正六边形的对称轴,设圆心为 $O$,连接 $OB$,$O$ 是线段 $CF$ 的中点,$\because$ 六边形 $ABCDEF$ 是正六边形,点 $O$ 是中心,$\therefore \angle BOC=\frac{360^{\circ}}{6}=60^{\circ}$,$\because OB = OC$,$\therefore \triangle BOC$ 是等边三角形,$\therefore OB = OC = BC$,在 $Rt\triangle BOG$ 中,$\angle BOG = 90^{\circ}-60^{\circ}=30^{\circ}$,设 $BG = x$,则 $OB = 2x$,$\therefore OG=\sqrt{OB^{2}-BG^{2}}=\sqrt{3}x$,$\therefore GH = 2OG = 2\sqrt{3}x$,在 $Rt\triangle EGH$ 中,$HE = x$,$GH = 2\sqrt{3}x$,$\therefore GE=\sqrt{GH^{2}+EH^{2}}=\sqrt{13}x$,
$\because CF = 2OB = 4x$,$\therefore \frac{GE}{CF}=\frac{\sqrt{13}}{4}$.

查看更多完整答案,请扫码查看


