《2025年5年中考3年模拟九年级数学下册湘教版》

1.(2022河北邯郸十一中期中)下列说法正确的是（M9202004）（ ）
A.过点A的圆的圆心可以是平面上任意一点
B.同一平面内,过A、B两点的圆的圆心在一条直线上
C.过A、B、C三点的圆的圆心有且只有一个
D.过A、B、C、D四点的圆不存在

答案： B：A.过点 A 的圆的圆心可以是平面上除 A 点外的任意一点，故本选项错误；B.在同一平面内，过 A、B 两点的圆的圆心在线段 AB 的垂直平分线上，故本选项正确；C.A、B、C 三点共线时，过 A、B、C 三点无法作圆，故本选项错误；D.过 A、B、C、D 四点的圆可能存在，故本选项错误. 故选 B.

2.教材变式·P63练习T2(2024广西百色期末)小明不慎把家里的圆形镜子打碎了(如图),其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的碎片应该是（M9202004）（ ）

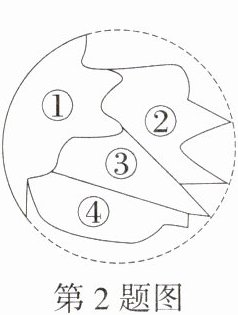
A.①
B.②
C.③
D.④

答案： A：碎片①上有一条弧，可在这条弧上任作两条不重合的弦，作出这两条弦的垂直平分线，两条垂直平分线的交点就是圆心，进而可得到半径. 故选 A.

3.(2023江苏宿迁泗洪二模)如图,在平面直角坐标系中,点A,B,C都在格点上,过A,B,C三点作一圆弧,则圆心的坐标是________.

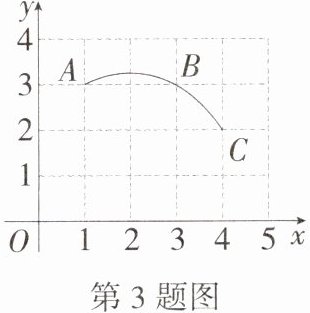
答案：
(2,1)
解析：作弦 AB 和 BC 的垂直平分线，交点即为圆心. 如图所示，圆心的坐标是(2,1).

4.(2024湖南师大附中星城实验中学月考)已知⊙O是△ABC的外接圆,那么点O一定是△ABC的（M9202004）（ ）
A.三个顶角的平分线的交点
B.三边高(或其所在直线)的交点
C.三边中线的交点
D.三边的垂直平分线的交点

答案： D：
∵⊙O 是△ABC 的外接圆，
∴OA = OB = OC，
∴点 O 是△ABC 的三边的垂直平分线的交点，故选 D.

5.[新独家原创]如图,⊙O为锐角△ABC的外接圆,有下列结论:①OA = OB = OC;②若∠A = 60°,则∠BOC = 120°;③若AB = AC,则直线OB⊥AC.其中错误结论的个数为（ ）

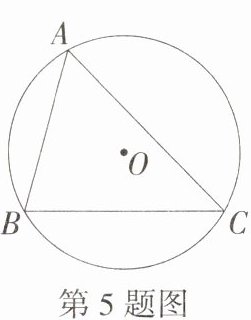
A.0
B.1
C.2
D.3

答案： B：
∵⊙O 为锐角△ABC 的外接圆，
∴OA = OB = OC，当∠A = 60°时，∠BOC = 2∠A = 120°，故结论①②正确. 若 AB = AC，则直线 OA⊥BC，直线 OB 不一定垂直于 AC，故结论③错误，故选 B.

6.[一题多解](2022湖南长沙长郡教育集团模拟)如图,⊙O为△ABC的外接圆,∠A = 45°,⊙O的半径为2,则BC的长为（ ）

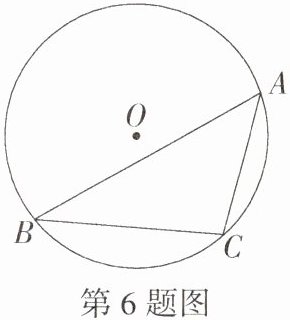
A.2
B.2$\sqrt{2}$
C.4
D.2$\sqrt{3}$

答案：
B
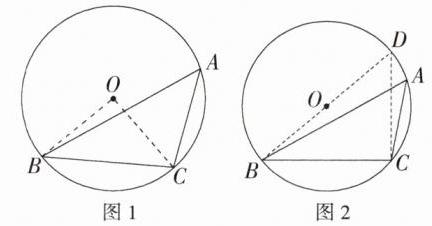
【解法一】如图 1，连接 OB，OC，
∵∠BAC = 45°，
∴∠BOC = 2∠BAC = 90°.
∵OB = OC = 2，
∴BC = $\sqrt{OB^{2}+OC^{2}}=2\sqrt{2}$. 故选 B.
【解法二】如图 2，连接 BO 并延长，交⊙O 于点 D，连接 DC，则∠BCD = 90°，∠D = ∠A = 45°，
∴BC = BD·sin D = 4×$\frac{\sqrt{2}}{2}=2\sqrt{2}$，故选 B.

7.(2024湖南师大附中月考)已知Rt△ABC中,∠A = 90°,AB = 6,AC = 8,则△ABC外接圆的半径 = ________.（M9202004）

答案： 5
解析：
∵∠A = 90°，AB = 6，AC = 8，
∴BC = $\sqrt{AB^{2}+AC^{2}} = 10$，
∴Rt△ABC 外接圆的半径 = $\frac{1}{2}BC = 5$.

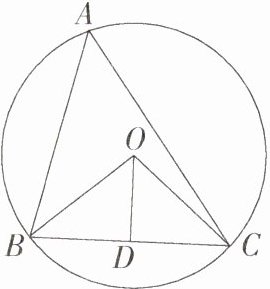
8.(2021湖南张家界中考)如图,△ABC内接于⊙O,∠A = 50°,D是BC的中点,连接OD,OB,OC,则∠BOD = ________.（M9202004）

答案： 50°
解析：
∵∠A = 50°，
∴∠BOC = 2∠A = 100°.
∵OB = OC，D 为 BC 的中点，
∴OD 平分∠BOC，
∴∠BOD = $\frac{1}{2}∠BOC = 50°$.

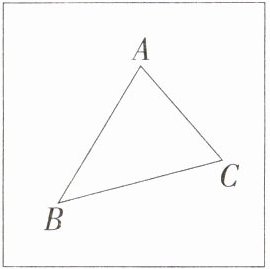
9.[新考向·尺规作图](2024辽宁沈阳模拟)小明家的房前有一块矩形空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).（M9202004）

答案：
解析：花坛的位置如图所示.