《2025年5年中考3年模拟九年级数学下册湘教版》

三、解答题(共46分)
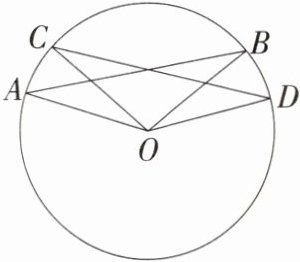
19.(2024江西南昌三中教育集团期中)(6分)如图,A、B、C、D是☉O上的点,且$\overset{\frown}{AC}=\overset{\frown}{BD}$,∠AOB = 125°,求∠COD的度数.

答案： 解析
∵$\overset{\frown}{AC}=\overset{\frown}{BD}$，$\overset{\frown}{AC}+\overset{\frown}{BC}=\overset{\frown}{AB}$，$\overset{\frown}{BD}+\overset{\frown}{BC}=\overset{\frown}{DC}$，
∴$\overset{\frown}{AB}=\overset{\frown}{DC}$，
∴$∠COD = ∠AOB = 125^{\circ}$.

20.(7分)如图,已知线段AB,求作以AB为直径的☉O及☉O的内接正六边形.(要求用直尺和圆规作图,保留作图痕迹,不必写作法和证明)

答案：
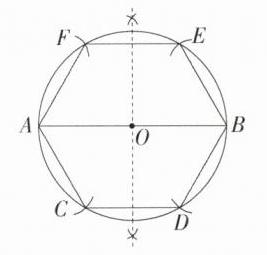
解析 如图所示，$⊙O$及正六边形ACDBEF即为所求.

21.(2022湖南邵阳中考)(7分)如图,DC是☉O的直径,点B为CD延长线上一点,AB是☉O的切线,点A为切点,且AB = AC.
(1)求∠ACB的度数.
(2)若☉O的半径为3,求$\overset{\frown}{AC}$的长.

答案： 解析
(1)连接OA(图略)，
∵AB是$⊙O$的切线，点A为切点，
∴$∠BAO = 90^{\circ}$.
∵$AB = AC$，$OA = OC$，
∴$∠B = ∠ACB = ∠OAC$.设$∠ACB = x^{\circ}$，则$∠B = ∠OAC = x^{\circ}$，
∴$x^{\circ}+x^{\circ}+x^{\circ}+90^{\circ}=180^{\circ}$，解得$x = 30$，
∴$∠ACB = 30^{\circ}$.
(2)由
(1)知$∠ACB = ∠OAC = 30^{\circ}$，
∴$∠AOC = 120^{\circ}$，
∴$\overset{\frown}{AC}$的长$=\frac{120\pi\times3}{180}=2\pi$.

22.(2024湖南衡阳八中教育集团期末)(8分)如图,AB是☉O的直径,点C,M是☉O上的点,且OM//BC,AC与OM,BM分别交于点E,F.
(1)求证:点M为$\overset{\frown}{AC}$的中点.
(2)若ME = 2,AC = 8,求☉O的直径.

答案： 解析
(1)证明：
∵AB是$⊙O$的直径，
∴$∠ACB = 90^{\circ}$.
∵$OM// BC$，
∴$∠OEA = ∠ACB = 90^{\circ}$，
∴$OM⊥AC$，
∴$\overset{\frown}{AM}=\overset{\frown}{CM}$，
∴点M为$\overset{\frown}{AC}$的中点.
(2)
∵$OM⊥AC$，
∴$AE=\frac{1}{2}AC = 4$.设$⊙O$的半径为r，则$OE = OM - ME = r - 2$.在$Rt\triangle AEO$中，$AO^{2}=AE^{2}+OE^{2}$，
∴$r^{2}=4^{2}+(r - 2)^{2}$，解得$r = 5$，
∴$⊙O$的直径为10.