《2025年5年中考3年模拟九年级数学下册湘教版》

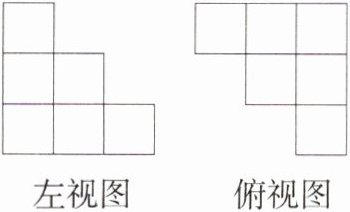
9.(2023四川眉山中考,8,★★☆)由相同的小正方体搭成的立体图形的部分视图如图所示,则搭成该立体图形的小正方体的个数最少为(M9203003) ( )

A.6
B.9
C.10
D.14

答案： B 结合左视图和俯视图可知搭成的立体图形有三层，最底层有 6 个小正方体，中间一层最少有 2 个小正方体，最上面一层最少有 1 个小正方体，则搭成该立体图形的小正方体的个数最少为 $6 + 2+1 = 9$.

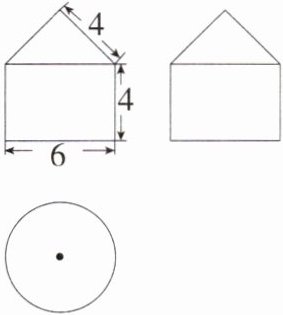
10.(2023山东济宁中考,8,★★☆)一个几何体的三视图如图所示,则这个几何体的表面积是(M9203003) ( )

A.39π
B.45π
C.48π
D.54π

答案： B 由三视图可知，原几何体是由一个圆锥和一个圆柱构成的，其中圆柱底面圆的直径为 6，高为 4，圆锥底面圆的直径为 6，母线长为 4，所以该几何体的表面积为 $\pi×(\frac{6}{2})^{2}+6\pi×4+\frac{1}{2}×6\pi×4 = 45\pi$.

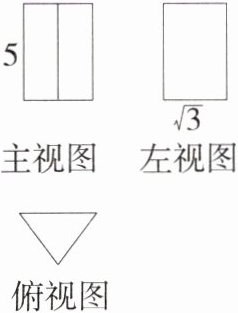
11.(2024湖南永州道县模拟,16,★★☆)某几何体的三视图如图所示,其中俯视图是等边三角形,则该几何体的侧面积是________.(M9203003)

答案：   30
解析 由三视图可知该几何体为直三棱柱，
∵ 等边三角形的高为 $\sqrt{3}$，
∴ 等边三角形的边长为 $\frac{\sqrt{3}}{\sin60^{\circ}} = 2$，
∴ 此直三棱柱的底面是边长为 2 的等边三角形，由题图可知直三棱柱的侧棱长为 5，则该几何体的侧面积是 $2×3×5 = 30$.

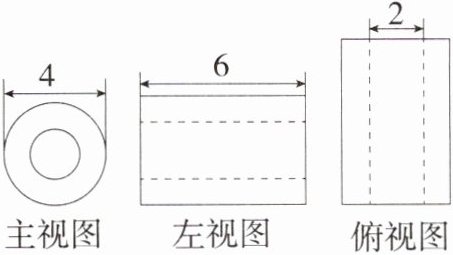
12.(2024广东河源紫金期末,14,★★☆)如图所示的是一个几何体的三视图,根据图中的数据可得这个几何体的体积为________.(结果保留π)(M9203003)

答案：   $18\pi$
解析 由题图可知，这个几何体是一个空心的圆柱，且圆柱体底面外圆的直径为 4，内圆直径为 2，高为 6，
∴ 这个几何体的体积为 $\pi×(\frac{4}{2})^{2}×6-\pi×(\frac{2}{2})^{2}×6=24\pi - 6\pi = 18\pi$.

13.(2024湖南衡阳模拟,16,★★☆)在一个仓库里堆积着正方体的货箱若干个,要搬运这些箱子很困难,可是仓库管理员要确认一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,如图所示.现要取走一些货箱,但要使剩余货箱的主视图不变,最多可以取走________个货箱.(M9203004)

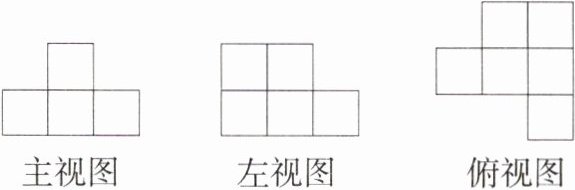
答案：
  4
解析 如图所示，俯视图中小正方形中的数字表示该位置上货箱的数量，
总共有 8 个货箱. 主视图中有 4 个货箱，故最多可以取走 $8 - 4 = 4$ 个货箱.

14.空间观念(2024山东青岛二十六中三模)一透明的敞口正方体容器装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE =α,如图1所示),此时液面刚好过棱CD,并与棱BB'交于点Q,此时液体的形状为直三棱柱,三视图及尺寸如图2所示,当正方体平放(正方形ABCD在桌面上)时,液体的深度是________dm.(M9203004)

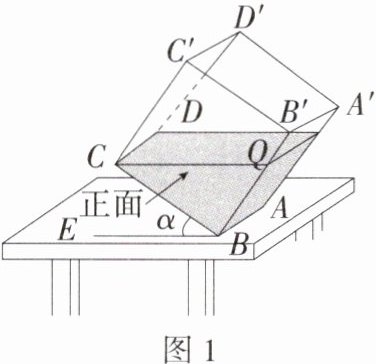
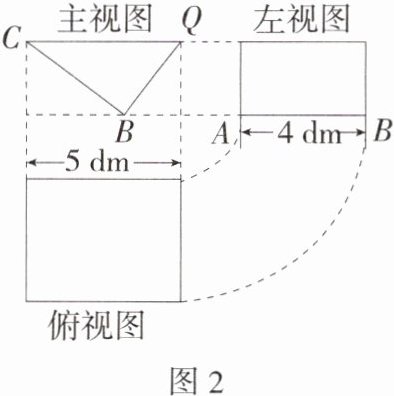
答案：   1.5
解析

∵ 容器是正方体，
∴ $BC = AB = 4\ dm$，$\angle CBQ = 90^{\circ}$，
∵ $CQ = 5\ dm$，
∴ $BQ=\sqrt{CQ^{2}-BC^{2}}=\sqrt{5^{2}-4^{2}} = 3(dm)$，
∴ 液体的体积 $=\frac{1}{2}×3×4×4 = 24(dm^{3})$，
∴ 当正方体平放时，液体的深度是 $24÷(4×4)=1.5(dm)$.