《2025年5年中考3年模拟九年级数学下册湘教版》

9.数形结合思想(2023湖南衡阳中考,12,★★☆)已知$m＞n＞0$,若关于$x$的方程$x^{2}+2x-3-m = 0$的解为$x_{1},x_{2}(x_{1}＜x_{2})$,关于$x$的方程$x^{2}+2x-3-n = 0$的解为$x_{3},x_{4}(x_{3}＜x_{4})$,则下列结论正确的是(M9201004) ( )
A.$x_{3}＜x_{1}＜x_{2}＜x_{4}$
B.$x_{1}＜x_{3}＜x_{4}＜x_{2}$
C.$x_{1}＜x_{2}＜x_{3}＜x_{4}$
D.$x_{3}＜x_{4}＜x_{1}＜x_{2}$

答案：
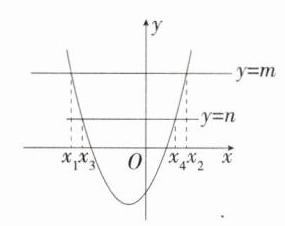
B 关于$x$的方程$x^{2}+2x-3-m = 0$的解为抛物线$y = x^{2}+2x-3$与直线$y = m$的交点的横坐标，关于$x$的方程$x^{2}+2x-3-n = 0$的解为抛物线$y = x^{2}+2x-3$与直线$y = n$的交点的横坐标，如图所示，$x_{1}＜x_{3}＜x_{4}＜x_{2}$，故选B.

10.新考向·新定义试题(2023湖南岳阳中考,8,★★☆)若一个点的坐标满足$(k,2k)$,我们将这样的点定义为“倍值点”.若关于$x$的二次函数$y=(t + 1)x^{2}+(t + 2)x + s(t,s$为常数,$t\neq-1)$的图象上总有两个不同的倍值点,则$s$的取值范围是(M9201004) ( )
A.$s＜-1$
B.$s＜0$
C.0＜s＜1
D.-1＜s＜0

答案： D 将$(k,2k)$代入，得$2k=(t + 1)k^{2}+(t + 2)k + s$，整理得$(t + 1)k^{2}+tk + s = 0$.根据题意可知关于$k$的二次方程$(t + 1)k^{2}+tk + s = 0$有两个不同的实数根，
∴$t^{2}-4s(t + 1)＞0$.令$g=t^{2}-4s(t + 1)=t^{2}-4st-4s$.
∵$g＞0$，
∴抛物线$g=t^{2}-4st-4s$的顶点的纵坐标大于0，即$\frac{-16s-16s^{2}}{4}＞0$，
∴$s(s + 1)＜0$，解得$-1＜s＜0$.故选D.

11.(2024四川广元中考,10,★★☆)如图,已知抛物线$y = ax^{2}+bx + c$过点$C(0,-2)$,与$x$轴交点的横坐标分别为$x_{1},x_{2}$,且$-1＜x_{1}＜0,2＜x_{2}＜3$,有下列结论:①$a - b + c＜0$;②方程$ax^{2}+bx + c + 2 = 0$有两个不相等的实数根;③$a + b＞0$;④$a＞\frac{2}{3}$;⑤$b^{2}-4ac＞4a^{2}$.其中正确的结论有(M9201003) ( )

A.1个
B.2个
C.3个
D.4个

答案： C
∵抛物线开口向上，$-1＜x_{1}＜0$，$2＜x_{2}＜3$，
∴当$x=-1$时，$y=a - b + c＞0$，故①中结论错误.已知抛物线$y = ax^{2}+bx + c$过点$C(0,-2)$，可知函数$y = ax^{2}+bx + c$的最小值小于-2，
∴$ax^{2}+bx + c=-2$有两个不相等的实数根，
∴方程$ax^{2}+bx + c + 2 = 0$有两个不相等的实数根，故②中结论正确.
∵$-1＜x_{1}＜0$，$2＜x_{2}＜3$，抛物线的对称轴为直线$x=-\frac{b}{2a}$，
∴$\frac{1}{2}＜-\frac{b}{2a}＜\frac{3}{2}$，
∴$1＜-\frac{b}{a}＜3$，
∵$a＞0$，
∴$-3a＜b＜-a$，
∴$a + b＜0$，故③中结论错误.
∵抛物线$y = ax^{2}+bx + c$过点$C(0,-2)$，
∴$c=-2$.
∵$x=-1$时，$y=a - b + c＞0$，
∴$3a-3b + 3c＞0$，
∵当$x = 3$时，$y=9a + 3b + c＞0$，
∴$(3a-3b + 3c)+(9a + 3b + c)=12a + 4c＞0$，
∴$12a＞8$，
∴$a＞\frac{2}{3}$，故④中结论正确.
∵$-1＜x_{1}＜0$，$2＜x_{2}＜3$，
∴$x_{2}-x_{1}＞2$，由根与系数的关系得$x_{1}+x_{2}=-\frac{b}{a}$，$x_{1}x_{2}=\frac{c}{a}$，
∴$\frac{b^{2}-4ac}{4a^{2}}=\frac{1}{4}\times(-\frac{b}{a})^{2}-\frac{c}{a}=\frac{1}{4}(x_{1}+x_{2})^{2}-x_{1}x_{2}=\frac{1}{4}[(x_{1}+x_{2})^{2}-4x_{1}x_{2}]=\frac{1}{4}(x_{1}-x_{2})^{2}＞\frac{1}{4}\times4 = 1$，
∴$b^{2}-4ac＞4a^{2}$，故⑤中结论正确.综上所述，②④⑤正确，共3个.故选C.

12.(2024四川南充中考,16,★★☆)已知抛物线$C_{1}:y = x^{2}+mx + m$与$x$轴交于两点$A,B(A$在$B$的左侧),抛物线$C_{2}:y = x^{2}+nx + n(m\neq n)$与$x$轴交于两点$C,D(C$在$D$的左侧),且$AB = CD$.下列四个结论:①抛物线$C_{1}$与$C_{2}$的交点坐标为$(-1,1)$;②$m + n = 4$;③$mn＞0$;④$A,D$两点关于点$(-1,0)$对称.其中正确的结论是______.(填写序号)(M9201004)

答案：  ①②④
解析 令$x^{2}+mx + m=x^{2}+nx + n(m\neq n)$，解得$x=-1$，把$x=-1$代入$y = x^{2}+mx + m$，得$y = 1$，
∴抛物线$C_{1}$与$C_{2}$的交点坐标为$(-1,1)$，故①正确.
∵抛物线$C_{1}:y = x^{2}+mx + m$与抛物线$C_{2}:y = x^{2}+nx + n$的开口方向和大小相同，且$AB = CD$，
∴两抛物线沿直线$x=-1$对折能够重合，
∴两抛物线关于直线$x=-1$对称，
∴$A$，$D$两点关于点$(-1,0)$对称，故④正确.
∵抛物线$C_{1}:y = x^{2}+mx + m$的对称轴为直线$x=-\frac{m}{2}$，抛物线$C_{2}:y = x^{2}+nx + n$的对称轴为直线$x=-\frac{n}{2}$，两抛物线关于直线$x=-1$对称，
∴$\frac{-\frac{m}{2}+(-\frac{n}{2})}{2}=-1$，$-\frac{m}{2}＞-1$，$-\frac{n}{2}＜-1$或$-\frac{n}{2}＞-1$，$-\frac{m}{2}＜-1$，
∴$m + n = 4$，$m＜2$，$n＞2$或$m＞2$，$n＜2$，
∴$mn＞0$不一定成立，故②正确，③错误.

13.几何直观(2022湖南衡阳中考)如图,已知抛物线$y = x^{2}-x-2$交$x$轴于$A、B$两点,将该抛物线位于$x$轴下方的部分沿$x$轴翻折,其余部分不变,得到的新图象记为“图象$W$”,图象$W$交$y$轴于点$C$.
(1)写出图象$W$位于$A,B$两点之间的部分对应的函数关系式.
(2)若直线$y=-x + b$与图象$W$有三个交点,请结合图象,直接写出$b$的值.
(3)$P$为$x$轴正半轴上一动点,过点$P$作$PM// y$轴交直线$BC$于点$M$,交图象$W$于点$N$,是否存在这样的点$P$,使$\triangle CMN$与$\triangle OBC$相似?若存在,求出所有符合条件的点$P$的坐标;若不存在,请说明理由.

答案：
解析
(1)当$x = 0$时，$y=-2$，
∴$C(0,2)$，
当$y = 0$时，$x^{2}-x-2 = 0$，解得$x_{1}=2$，$x_{2}=-1$，
∴点$A(-1,0)$，点$B(2,0)$，
设图象$W$的表达式为$y=a(x + 1)(x - 2)(-1＜x＜2)$，
把$(0,2)$代入，得$-2a = 2$，
∴$a=-1$，
∴$y=-(x + 1)(x - 2)=-x^{2}+x + 2$，
∴图象$W$位于$A$，$B$两点之间的部分对应的函数关系式为$y=-x^{2}+x + 2(-1＜x＜2)$.
(2)由图象得直线$y=-x + b$与图象$W$有三个交点时，存在两种情况：
①直线$y=-x + b$过点$B$，此时$b = 2$.
②直线$y=-x + b$与$y=-x^{2}+x + 2$的图象只有一个交点，如图1，
令$-x + b=-x^{2}+x + 2$，整理，得$x^{2}-2x + b-2 = 0$，
此时$\Delta=(-2)^{2}-4\times1\times(b - 2)=0$，
∴$b = 3$.
综上，$b$的值是2或3.

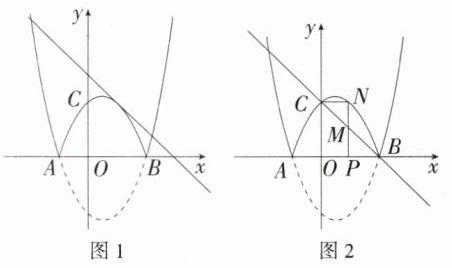
(3)
∵$OB = OC = 2$，$\angle BOC = 90^{\circ}$，
∴$\triangle BOC$是等腰直角三角形.分情况讨论：①如图2，当$CN// OB$时，$\triangle CNM\sim\triangle BOC$，
当$y = 2$时，$-x^{2}+x + 2 = 2$，解得$x = 0$或$x = 1$.
∵$PN// y$轴，
∴点$P$的坐标为$(1,0)$.
②如图3，当$CN// OB$时，$\triangle CNM\sim\triangle BOC$，
当$y = 2$时，$x^{2}-x-2 = 2$，解得$x_{1}=\frac{1+\sqrt{17}}{2}$，$x_{2}=\frac{1-\sqrt{17}}{2}$(舍去)，
∴点$P$的坐标为$(\frac{1+\sqrt{17}}{2},0)$.

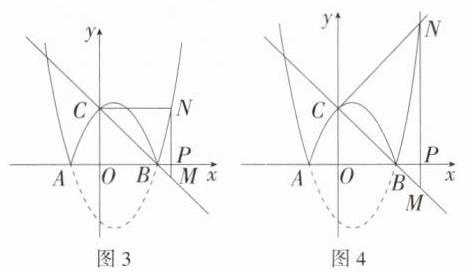
③如图4，当$\angle MCN = 90^{\circ}$时，$\triangle OBC\sim\triangle CMN$，
易得直线$CN$的解析式为$y = x + 2$，
令$x + 2=x^{2}-x-2$，解得$x_{1}=1+\sqrt{5}$，$x_{2}=1-\sqrt{5}$(舍去)，
∴点$P$的坐标为$(1+\sqrt{5},0)$.
综上可知，点$P$的坐标为$(1,0)$或$(\frac{1+\sqrt{17}}{2},0)$或$(1+\sqrt{5},0)$.