《2025年5年中考3年模拟九年级数学下册湘教版》

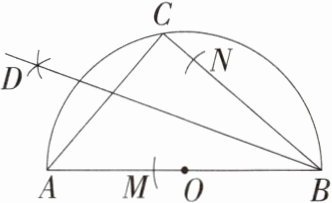
10.(2024湖北中考,8,★☆☆)如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB = 50°,则∠CBD的度数是 (M9202002) ( )

A.30°
B.25°
C.20°
D.15°

答案： C

∵AB是半圆O的直径，
∴∠ACB = 90°，
∵∠CAB = 50°，
∴∠ABC = 90° - 50° = 40°．由尺规作图可知BD为∠ABC的平分线，
∴∠CBD = ∠ABD = $\frac{1}{2}$∠ABC = 20°．故选C．

11.易错题(2024江苏南京一中月考,15,★☆☆)在半径为5的圆中,长度为5$\sqrt{3}$的弦所对圆周角的度数是________.(M9202002)

答案：
  60°或120°
解析 如图，在⊙O中，半径为5，AB = 5$\sqrt{3}$，连接OA，OB，过O点作OH⊥AB于点H，
∵OA = OB，
∴AH = BH = $\frac{1}{2}$AB = $\frac{5\sqrt{3}}{2}$，∠AOH = ∠BOH．
∵OA = 5，
∴sin∠AOH = $\frac{AH}{OA}$ = $\frac{\sqrt{3}}{2}$，
∴∠AOH = 60°，
∴∠AOB = 2∠AOH = 120°．
∵弦AB所对的弧有两条，
∴弦AB所对的圆周角有两个．①当顶点在优弧上时，如点C，∠C = $\frac{1}{2}$∠AOB = 60°．②当顶点在劣弧上时，如点D，∠D = 180° - ∠C = 180° - 60° = 120°．综上可知，该弦所对圆周角的度数是60°或120°．

·易错警示
一条弦所对的圆周角有两种情况，一种是顶点在优弧上，另一种是顶点在劣弧上．

12.(2024湖南常德安乡期末,23,★★☆)如图,AB、AC是⊙O的两条弦,点D是$\overset{\frown}{BC}$的中点,连接并延长BD、CD,分别交AC、AB的延长线于点E、F,且DF = DE.(M9202002)
(1)求证:AC = AB;
(2)若BD = 3,CE = 4,求⊙O的半径.

答案： 解析
(1)证明：
∵点D是$\overset{\frown}{BC}$的中点，
∴CD = BD．
在△CED和△BFD中，$\begin{cases}CD = BD,\\\angle CDE = \angle BDF,\\DE = DF,\end{cases}$
∴△CED≌△BFD(SAS)，
∴∠E = ∠F．
∵CF = CD + DF，BE = BD + DE，
∴BE = CF．
在△CAF和△BAE中，$\begin{cases}\angle A = \angle A,\\\angle F = \angle E,\\CF = BE,\end{cases}$
∴△CAF≌△BAE(AAS)，
∴AC = AB．
(2)连接AD，由△CAF≌△BAE可得∠ACD = ∠ABD，
∵四边形ABDC是圆内接四边形，
∴∠ACD + ∠ABD = 180°，
∴∠ACD = ∠ABD = 90°，
∴AD是⊙O的直径，∠DCE = 90°．
∵CD = BD = 3，CE = 4，
∴DE = $\sqrt{CD^{2}+CE^{2}}$ = 5，
∴EB = 5 + 3 = 8．设AB = AC = x，则AE = x + 4，
在Rt△ABE中，AB² + BE² = AE²，
∴x² + 8² = (x + 4)²，解得x = 6，
∴AB = 6，
在Rt△ABD中，AD = $\sqrt{6^{2}+3^{2}}$ = 3$\sqrt{5}$，
∴⊙O的半径为$\frac{3\sqrt{5}}{2}$．

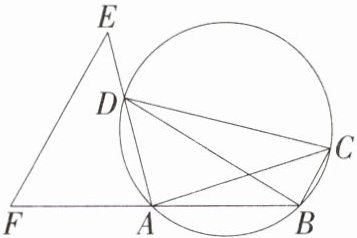
13.推理能力(2024浙江中考)如图,在圆内接四边形ABCD中,AD＜AC,∠ADC＜∠BAD,延长AD至点E,使AE = AC,延长BA至点F,连接EF,使∠AFE = ∠ADC.(M9202002)
(1)若∠AFE = 60°,CD为直径,求∠ABD的度数.
(2)求证:①EF//BC;②EF = BD.

答案：
解析
(1)
∵CD为直径，
∴∠CAD = 90°．
∵∠ADC = ∠AFE = 60°，
∴∠ACD = 90° - 60° = 30°，
∴∠ABD = ∠ACD = 30°．
(2)证明：①如图，延长AB得到射线AM，
∵四边形ABCD是圆内接四边形，
∴∠CBM = ∠ADC，
又
∵∠AFE = ∠ADC，
∴∠AFE = ∠CBM，
∴EF//BC．

②如图，过点D作DG//BC交⊙O于点G，连接AG，则DG//BC//EF，
∴∠FED = ∠EDG，∠CDG = ∠BCD，
∴$\overset{\frown}{BD}=\overset{\frown}{CG}$，
∴BD = CG，
∵四边形ACGD是圆内接四边形，
∴∠GDE = ∠ACG，
∴∠FED = ∠ACG，
∵∠AFE = ∠ADC，∠ADC = ∠AGC，
∴∠AFE = ∠AGC，
∵AE = AC，
∴△AEF≌△ACG(AAS)，
∴EF = CG，
∴EF = BD．

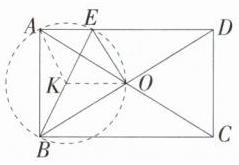
1.(2024四川凉山州会东二模)如图,矩形ABCD的对角线相交于O点,过点O作OE⊥BD,交AD于点E,连接BE,若∠ABE = 20°,则∠AOE的大小是 ( )

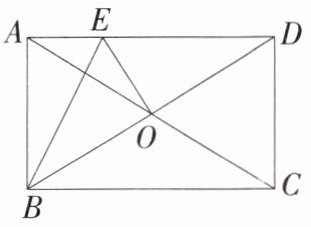
A.10° B.15° C.20° D.30°

答案：
C 如图，取BE的中点K，连接AK、OK．
∵四边形ABCD是矩形，
∴∠BAE = 90°，
∵EO⊥BD，
∴∠BOE = 90°，
∴四边形ABOE对角互补，
∴A、B、O、E四点共圆，
∴∠AOE = ∠ABE = 20°，故选C．

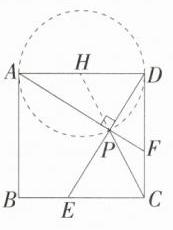
2.(2024湖南邵阳邵东三模)如图,点E是正方形ABCD的边BC上一动点(点E不与点B、C重合),连接DE,过点A作AF⊥DE交CD于点F,垂足为点P,连接PC,已知正方形的边长为2,则PC的最小值为________.

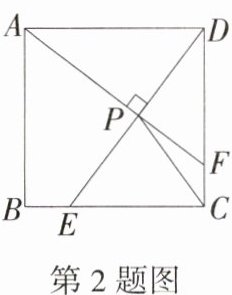
答案：
  $\sqrt{5}-1$
解析

∵AF⊥DE，
∴∠APD = 90°，
∴点P的运动轨迹是以AD为直径的圆的一段弧，如图，取AD的中点H，以AD为直径作⊙H，连接CH，交⊙H于点P，则PC的长即为所求，
∵正方形的边长为2，
∴DC = 2，DH = 1，
∴CH = $\sqrt{2^{2}+1^{2}}$ = $\sqrt{5}$，
∵HP = 1，
∴CP = $\sqrt{5}-1$．

3.(2024湖南娄底二中二模)如图,在矩形ABCD中,AB = 10,BC = 12,E是矩形内部的一个动点,且满足∠BAE = ∠CBE,则线段CE长度的最小值为________.

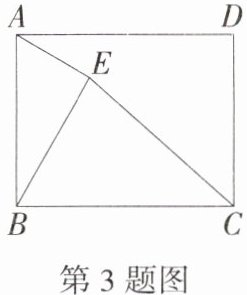
答案：
  8
解析

∵∠BAE = ∠CBE，∠CBE + ∠ABE = 90°，
∴∠BAE + ∠ABE = 90°，
∴∠AEB = 90°，
∴点E在以AB为直径的圆上，如图，取AB的中点O，连接OC交圆于E'，当E与E'重合时，线段CE的长最小，
∵AB = 10，
∴OB = OA = OE' = 5，
∵BC = 12，
∴OC = $\sqrt{OB^{2}+BC^{2}}$ = 13，
∴CE' = OC - OE' = 13 - 5 = 8，
∴线段CE长度的最小值为8．